练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．求值：cos415°-sin415°=$\frac{\sqrt{3}}{2}$．

    分析 利用平方差公式，二倍角的余弦公式，求得所给式子的值．

    解答 解：cos415°-sin415°=（cos215°+sin215°）•（cos215°-sin215°）
    =cos215°-sin215°=cos30°=$\frac{\sqrt{3}}{2}$，
    故答案为：$\frac{{\sqrt{3}}}{2}$．

    点评 本题主要考查平方差公式，二倍角的余弦公式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．已知函数f（x）=x2（2x-2-x），则不等式f（2x+1）+f（1）＜0的解集是（　　）
    A．$（{-∞，-\frac{1}{2}}）$B．（-∞，-1）C．$（{-\frac{1}{2}，+∞}）$D．（-1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知集合A={x|1＜x＜3}，B={x|2m＜x＜1-m}，其中m＜$\frac{1}{3}$．
    （1）当m=-1时，求A∪B；
    （2）若A⊆B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．一家商场为了确定营销策略，进行了投入促销费用x和商场实际销售额y的试验，得到如下四组数据．
    投入促销费用x（万元）2356
    商场实际营销额y（万元）100200300400
    （1）求出x，y之间的回归直线方程$\widehaty$=$\widehatb$x+$\widehata$；
    （2）若该商场计划营销额不低于600万元，则至少要投入多少万元的促销费用？
    （注：$b=\frac{{\sum _{i=1}^n（{{x_i}-\bar x}）（{{y_i}-\bar y}）}}{{\sum _{i=1}^n{{（{{x_i}-\bar x}）}^2}}}=\frac{{\sum _{i=1}^n{x_i}{y_i}-n•\bar x•\bar y}}{{\sum _{i=1}^nx_i^2-n•{{\bar x}^2}}}，a=\bar y-b•\bar x$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an}的前n项和为Sn，a1=1，an≠0，anan+1=4Sn-1．
    （1）求{an}的通项公式；
    （2）若数列{bn}满足$\frac{{a}_{n}}{{b}_{n}}$=2n-1（n∈N*），设Tn是数列{bn}的前n项和，证明Tn＜6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知递增数列{an}，a1=2，其前n项和为Sn，且满足${a_n}^2+2=3（{S_n}+{S_{n-1}}）（n≥2）$．
    （1）求a2的值；
    （2）求数列{an}的通项公式；
    （3）若数列{bn}满足${log_2}\frac{b_n}{a_n}=n$，求其前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

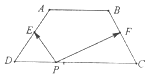    3．如图，梯形ABCD中，AB∥CD，AB=2，CD=4，BC=AD=$\sqrt{5}$，E和F分别为AD与BC的中点，对于常数λ，在梯形ABCD的四条边上恰好有8个不同的点P，使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立，则实数λ的取值范围是（　　）
    A．（-$\frac{5}{4}$，-$\frac{9}{20}$）B．（-$\frac{5}{4}$，$\frac{11}{4}$）C．（-$\frac{1}{4}$，$\frac{11}{4}$）D．（-$\frac{9}{20}$，-$\frac{1}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设两个非零向量$\vec a$与$\vec b$不共线．
    （1）若$\overrightarrow{AB}=\vec a+\vec b，\overrightarrow{BC}=2\vec a+8\vec b，\overrightarrow{CD}=3（{\vec a-\vec b}）$，求证：A，B，D三点共线
    （2）试确定实数k，使$k\vec a+\vec b$和$\vec a+k\vec b$反向共线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在△ABC中，若sinA：sinB：sinC=3：5：7，则cosC=-$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案