
分析 (1)运用二次方程实根分布的表示,可得不等式组,注意判别式大于0,对称轴介于0和1,端点的函数值大于0,画出不等式组表示的区域,由三点代入即可得到所求范围;
(2)(i)由0<x1<x2<1,λ>0,作差比较,化简即可得证;
(ii)由x1=f(x1),t-x1>0,x1+a=1-x2>0,作差比较可得x1<f(t);同理可得f(t)<x2.
解答 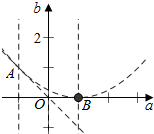 解:(1)由题意可得x1,x2为方程x2+(a-1)x+b=0的两根,
解:(1)由题意可得x1,x2为方程x2+(a-1)x+b=0的两根,
即有x1+x2=1-a,x1x2=b,
由x1,x2∈(0,1),可得
$\left\{\begin{array}{l}{b>0}\\{a+b>0}\\{0<-\frac{a-1}{2}<1}\\{(a-1)^{2}-4b>0}\end{array}\right.$,画出(a,b)表示的可行域,如右OAB表示的部分:
又f($\frac{1}{2}$)=$\frac{1}{4}$+$\frac{1}{2}$a+b,将A(-1,1)代入f($\frac{1}{2}$)可得$\frac{3}{4}$;
将(0,0)代入,可得$\frac{1}{4}$;将B(1,0)代入f($\frac{1}{2}$)可得$\frac{3}{4}$.
综上可得,f($\frac{1}{2}$)的取值范围为($\frac{1}{4}$,$\frac{3}{4}$);
(2)证明:(i)由0<x1<x2<1,λ>0,
可得t-x1=$\frac{{x}_{1}+λ{x}_{2}}{1+λ}$-x1=$\frac{λ({x}_{2}-{x}_{1})}{1+λ}$>0,
即有t>x1;
t-x2=$\frac{{x}_{1}+λ{x}_{2}}{1+λ}$-x2=$\frac{{x}_{1}-{x}_{2}}{1+λ}$<0,
即有t<x2.
综上可得,x1<t<x2;
(ii)由x1=f(x1),t-x1>0,x1+a=1-x2>0,
可得f(t)-x1=f(t)-f(x1)=t2+at+b-x12-ax1-b
=(t-x1)(t+x1+a)>0,
可得f(t)>x1;
同样f(t)-x2=f(t)-f(x2)=t2+at+b-x22-ax2-b
=(t-x2)(t+x2+a)<0,
可得f(t)<x2.
综上可得,x1<f(t)<x2.
点评 本题考查二次函数和方程的关系,考查实根分布的表示,注意运用判别式和对称轴方程,同时考查不等式的证明,注意运用作差法,考查推理和运算能力,属于中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6e2-6 | B. | 3e2-3 | C. | ex-1 | D. | e2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12\sqrt{5}}{5}$+1 | B. | $\frac{11\sqrt{5}}{5}$ | C. | 5 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2008 | B. | 2015 | C. | 2016 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
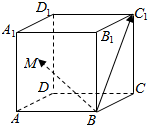 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1] | B. | [-2,1) | C. | [-2,1] | D. | [1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com