练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知y＝f(x)为定义在R上的奇函数，当x＞0时，f(x)＝|x2－4x＋3|，那么当x＜0时，f(x)＝

    [　　]
    A．

    －|x2＋4x＋3|

    B．

    －|x2－4x＋3|

    C．

    |－x2－4x＋3|

    D．

    －|－x2－4x＋3|

    答案：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高三数学教学与测试 题型：044

    已知曲线C的方程是(t＋1)＋2at)x＋3at＋b＝0，直线l的

    方程是y＝t(x－1)，若对任意实数t，曲线C恒过定点P(1，0)．

    (1)求定值a，b；

    (2)直线l截曲线C所得弦长为d，记f(t)＝，则当t为何值时，f(t)有最大值，最大值是多少？

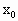    (3)若点M()在曲线C上，又在直线l上，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    已知：如图射线OA为y＝kx(k＞0，x＞0)，射线OB为y＝－kx(x＞0)，动点P(x，y)在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积恰为k．

    (Ⅰ)当k为定值时，动点P的纵坐标y是其横坐标x的函数，求这个函数y＝f(x)的解析式；

    (Ⅱ)根据k的取值范围，确定y＝f(x)的定义域．

    查看答案和解析>>

    科目：高中数学 来源：山东省淄博市2010届高三第二次模拟考试数学文科 题型：044

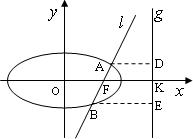
    如图，已知直线l：x＝my＋1过椭圆C：＝1的右焦点F，抛物线：x2＝4y的焦点为椭圆C的上顶点，且直线l交椭圆C于A、B两点，点A、F、B在直线g：x＝4上的射影依次为点D、K、E．

    (Ⅰ)求椭圆C的方程；

    (Ⅱ)若直线l交y轴于点M，且，当m变化时，探求λ1＋λ2的值是否为定值？若是，求出λ1＋λ2的值，否则，说明理由；

    (Ⅲ)连接AE、BD，试证明当m变化时，直线AE与BD相交于定点N．

    查看答案和解析>>

    科目：高中数学 来源：河南省豫南九校2012届高三第四次联考数学文科试题 题型：044

    已知函数f(x)＝lnx2－，(a∈R，e为自然对数的底数)．

    (Ⅰ)求函数f(x)的递增区间；

    (Ⅱ)当a＝1时，过点P(0，t)(t∈R)作曲线y＝f(x)的两条切线，设两切点为P1(x1，f(x1))，P2(x2，f(x2))(x1≠x2)，求证x1＋x2为定值，并求出该定值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年河北省石家庄市高三下学期第二次质量检测文科数学试卷（解析版） 题型：解答题

    (本小题满分12分）

    已知直线l1：4x:－3y＋6=0和直线l2：x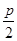＝－，.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.

    (I )求抛物线C的方程；

    (II)直线l过抛物线C的焦点F与抛物线交于A，B两点，且AA1，BB1都垂直于直线l2，垂足为A1，B1，直线l2与y轴的交点为Q，求证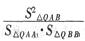：为定值。

     

    查看答案和解析>>

    同步练习册答案