
| A. | [$\sqrt{7}$-1,$\sqrt{7}$+1] | B. | ($\sqrt{7}$-1,$\sqrt{7}$+1) | C. | [1,2] | D. | (1,2) |
分析 利用向量的数量积运算性质和模的计算公式及不等式的性质即可得出
解答 解:∵向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,($\overrightarrow{a}-\overrightarrow{c}$)•($\overrightarrow{b}-\overrightarrow{c}$)=0,如图
∴设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,则$\overrightarrow{CA}=\overrightarrow{a}-\overrightarrow{c}$,$\overrightarrow{CB}=\overrightarrow{b}-\overrightarrow{c}$,所以CA⊥CB,如图,OA=OB=2,取AB中点D,设CD=x,则AB=2x,
则OD⊥AB,AO2=DO2+AD2,所以DO=$\sqrt{4-{x}^{2}}$,根据CD-CO≤OD≤CO+CD,
∴1-x$≤\sqrt{4-{x}^{2}}≤$1+x,解得$\frac{\sqrt{7}-1}{2}≤x≤\frac{\sqrt{7}+1}{2}$,
∴$\overrightarrow{a}-\overrightarrow{b}$=2x∈[$\sqrt{7}-1,\sqrt{7}+1$].
故选A.
点评 本题考查了向量的运算;借助于三角形法则等是解答的关键;要熟练掌握数量积运算性质、模的计算公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
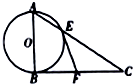 如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com