
���� ��1�����ü�������ֱ������Ļ�������д��ԲC��ֱ�����귽�̣����õ�P���ڼ���ԳƵĵ�P'�ļ�����Ϊ$��\sqrt{2}��\frac{5��}{4}��$���õ���P�ļ����ꣻ
��2����ֱ��I��ԲC�ཻ������A��B����$\left\{\begin{array}{l}x=1+t\\ y=1+\sqrt{3}t\end{array}\right.$����x2+y2=4���ã�$|{t_1}{t_2}|=\frac{1}{2}$���������P��A��B����ľ���֮����
��� �⣺��1��ԲC�ļ����귽��Ϊ��=2��ֱ�����귽��Ϊx2+y2=4��
��P���ڼ���ԳƵĵ�P'�ļ�����Ϊ$��\sqrt{2}��\frac{5��}{4}��$����P��$\sqrt{2}��\frac{��}{4}$����
��2����P��Ϊֱ������ΪP��1��1��
��$\left\{\begin{array}{l}x=1+t\\ y=1+\sqrt{3}t\end{array}\right.$����x2+y2=4���ã�$|{t_1}{t_2}|=\frac{1}{2}$��
���ԣ���P��A��B����ľ���֮��$\frac{1}{2}$��
���� ���⿼�鼫������ֱ������Ļ���������������̵����ã���������ļ������壬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x0∉∁RQ��x03��Q | B�� | ?x0��∁RQ��x03��Q | C�� | ?x∉∁RQ��x3��Q | D�� | ?x��∁RQ��x3∉Q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
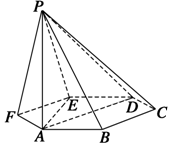 ��ͼ����֪����P-ABCDEF�ĵ������������Σ�PA��ƽ��ABC��PA=2AB�������н�����ȷ������Ǣܣ�
��ͼ����֪����P-ABCDEF�ĵ������������Σ�PA��ƽ��ABC��PA=2AB�������н�����ȷ������Ǣܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\sqrt{7}$-1��$\sqrt{7}$+1] | B�� | ��$\sqrt{7}$-1��$\sqrt{7}$+1�� | C�� | [1��2] | D�� | ��1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com