
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 根据所给的等差数列的S16>0且S17<0,根据等差数列的前n项和公式,看出第9项小于0,第8项和第9项的和大于0,得到第8项大于0,这样前8项的和最大.
解答 解:∵等差数列{an}中,S16>0且S17<0,
即S16=$\frac{16{(a}_{1}+{a}_{16})}{2}=8({a}_{8}+{a}_{9})>0$,
S17=$\frac{17({a}_{1}+{a}_{17})}{2}$=17a9<0,
∴a8+a9>0,a9<0,
∴a8>0,
∴数列的前8项和最大.
故答案为:8.
点评 本题考查等差数列的性质和前n项和,以及等差数列的性质,解题的关键是熟练运用等差数列的性质得出已知数列的项的正负.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{4}$) | B. | (2,+∞) | C. | (-2,$\frac{1}{4}$) | D. | (-∞,2)∪($\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
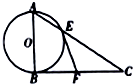 如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com