
| A. | (-∞,$\frac{1}{4}$) | B. | (2,+∞) | C. | (-2,$\frac{1}{4}$) | D. | (-∞,2)∪($\frac{1}{4}$,+∞) |
分析 先根据导数的几何意义写出函数f(x)在点A、B处的切线方程,再利用两直线重合的充要条件:斜率相等且纵截距相等,列出关系式,从而得出a=$\frac{1}{4}$(t4-2t2-8t+1),可得出a的取值范围.
解答 解:当x<0时,f(x)=x2+x+a的导数为f′(x)=2x+1;
当x>0时,f(x)=-$\frac{1}{x}$的导数为f′(x)=$\frac{1}{{x}^{2}}$,
设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2,
当x1<x2<0,或0<x1<x2时,f′(x1)≠f′(x2),故x1<0<x2,
当x1<0时,函数f(x)在点A(x1,f(x1))处的切线方程为
y-(x12+x1+a)=(2x1+1)(x-x1);
当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为y+$\frac{1}{{x}_{2}}$=$\frac{1}{{{x}_{2}}^{2}}$(x-x2).
两直线重合的充要条件是$\frac{1}{{{x}_{2}}^{2}}$=2x1+1①,-$\frac{2}{{x}_{2}}$=-x12+a②,
由①及x1<0<x2得0<$\frac{1}{{x}_{2}}$<1,由①②令t=$\frac{1}{{x}_{2}}$,则0<t<1,且a=$\frac{1}{4}$(t4-2t2-8t+1)在(0,1)为减函数,
∴-2<a<$\frac{1}{4}$,
故选:C.
点评 本题主要考查了导数的几何意义等基础知识,考查了推理论证能力、运算能力、创新意识,考查了函数与方程、分类与整合、转化与化归等思想方法.


科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2}-6\sqrt{2},-\frac{1}{2}+6\sqrt{2}}]$ | B. | [-6,6] | C. | $[{-\frac{1}{2}-3\sqrt{2},-\frac{1}{2}+3\sqrt{2}}]$ | D. | [-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
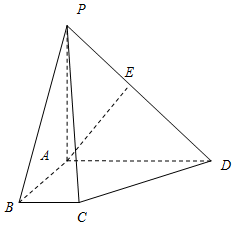 在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AP⊥BC,AB=BC=1,AD=AP=2,E是PD的中点.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,PA⊥底面ABCD,∠BAD=90°,AP⊥BC,AB=BC=1,AD=AP=2,E是PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com