
分析 由等差数列的性质,知$\frac{{{a_{10}}}}{{{b_9}+{b_{12}}}}$+$\frac{{{a_{11}}}}{{{b_8}+{b_{13}}}}$=$\frac{{a}_{10}+{a}_{11}}{{b}_{9}+{b}_{12}}$=$\frac{{a}_{10}+{a}_{11}}{{b}_{10}+{b}_{11}}$=$\frac{{S}_{20}}{{T}_{20}}$由此能够求出结果.
解答 解:∵数列{an}和{bn}都是等差数列,
∴$\frac{{{a_{10}}}}{{{b_9}+{b_{12}}}}$+$\frac{{{a_{11}}}}{{{b_8}+{b_{13}}}}$=$\frac{{a}_{10}+{a}_{11}}{{b}_{9}+{b}_{12}}$=$\frac{{a}_{10}+{a}_{11}}{{b}_{10}+{b}_{11}}$=$\frac{{S}_{20}}{{T}_{20}}$=$\frac{7×20}{20+3}$=$\frac{140}{23}$.
故答案是:$\frac{140}{23}$.
点评 本题考查等差数列的通项公式和前n项和公式的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
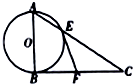 如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com