
分析 α是第二象限角,点P(x,$\sqrt{5}$)是α终边上一点,且cosα=$\frac{\sqrt{2}}{4}$x,可得$\frac{x}{\sqrt{{x}^{2}+5}}$=$\frac{\sqrt{2}x}{4}$,x<0,解得x.再利用三角函数的定义、诱导公式即可得出.
解答 解:∵α是第二象限角,点P(x,$\sqrt{5}$)是α终边上一点,且cosα=$\frac{\sqrt{2}}{4}$x,
∴$\frac{x}{\sqrt{{x}^{2}+5}}$=$\frac{\sqrt{2}x}{4}$,x<0,解得x=$-\sqrt{3}$.
∴P$(-\sqrt{3},\sqrt{5})$,∴cosα=-$\frac{\sqrt{6}}{4}$,sinα=$\frac{\sqrt{5}}{2\sqrt{2}}$=$\frac{\sqrt{10}}{4}$,tanα=$-\frac{\sqrt{10}}{\sqrt{6}}$=$-\frac{\sqrt{15}}{3}$.
∴4cos(α+$\frac{π}{2}$)-3tan α=-4sinα-3tanα=-4×$\frac{\sqrt{10}}{4}$-3×$\frac{\sqrt{15}}{-3}$=$\sqrt{15}$-$\sqrt{10}$.
故答案为:$\sqrt{15}$-$\sqrt{10}$.
点评 本题考查了三角函数的定义、诱导公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
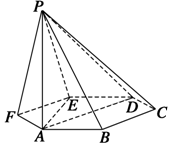 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的序号是④.
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的序号是④.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 31 | C. | 32 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.62 | B. | 0.68 | C. | 0.02 | D. | 0.38 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com