
分析 (Ⅰ)由a=1,b=0,得出f(x)的解析式,求切线方程,即先求f′(x)在x=1出的值为切线的斜率.由点斜式求出切线方程即可.
(Ⅱ)不等式2f(x)>3x2+a等价于(2x2-4ax)lnx+x2-a>0.
方法一:需要分类讨论,根据导数和函数最值得关系即可求出a的范围,
方法二:先求出a的范围,再验证即可.
解答 解:(Ⅰ)当a=1,b=0时,f(x)=(x2-2x)lnx,则f(1)=0,
∴f'(x)=(2x-x)lnx+x-2,
∴f(1)=-1.
∴曲线y=f(x)在点(1,f(1))处的切线方程为y=-(x-1),
即x+y-1=0.
(Ⅱ)当b=2时,f(x)=(x2-2ax)lnx+2x2,a∈R.
∴不等式2f(x)>3x2+a等价于(2x2-4ax)lnx+x2-a>0.
方法一:令p(x)=(2x2-4ax)lnx+x2-a,x∈[1,+∞),
则p'(x)=(4x-4a)lnx+(2x-4a)+2x=4(x-a)(lnx+1)(x≥1).
当a≤1时,p'(x)≥0,则函数p(x)在[1,+∞)上单调递增,
∴p(x)min=p(1)=1-a,
∴根据题意,知有1-a>0,∴a<1.
当a>1时,由p'(x)<0,知函数p(x)在[1,a)上单调增减;
由p'(x)>0,知函数p(x)在(a,+∞)上单调递增.
∴$p{(x)_{min}}=p(a)={a^2}(1-2lna)-a$.)
由条件知,a2(1-2lna)-a>0,即a(1-2lna)-1>0.
设q(a)=a(1-2lna)-1,a>1,则q'(a)=-1-2lna<0,a>1,
∴q(a)在(1,+∞)上单调递减.
又q(1)=0,所以q(a)<q(1)=0与条件矛盾.
综上可知,实数a的取值范围为(-∞,1).
方法二:令p(x)=(2x2-4ax)lnx+x2-a,x∈[1,+∞),
则p(x)=(2x2-4ax)lnx+x2-a>0在[1,+∞)上恒成立,
∴p(1)=1-a>0,
∴a<1.
又p'(x)=(4x-4a)lnx+(2x-4a)+2x=4(x-a)(lnx+1)(x≥1),
显然当a<1时,p'(x)>0,则函数p(x)在[1,+∞)上单调递增,
∴p(x)min=p(1)=1-a>0,
∴a<1.
综上可知a的取值范围为(-∞,1).
点评 本题考查了导数和几何意义以及导数和函数的最值的问题,以及参数的取值范围,属于中档题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
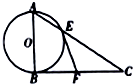 如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆交AC于点E,过点E作圆O的切线交BC于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | -$\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | { 3 } | C. | {2,4,6} | D. | {1,2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com