
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | -$\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
分析 由题意画出图形,设△ABC的外接圆半径为R,根据三角形外心的性质可得:OD⊥AB、OE⊥AC,由向量的线性运算和向量数量积的运算,求出$\overrightarrow{AB}•\overrightarrow{OA}$和$\overrightarrow{AC}•\overrightarrow{OA}$,在已知的等式两边同时与$\overrightarrow{OA}$进行数量积运算,代入后由正弦定理化简,由两角和的正弦公式和内角和定理求出λ的值.
解答 解:如图所示:O是锐角△ABC的外心,
D、E分别是AB、AC的中点,且OD⊥AB,OE⊥AC,
设△ABC外接圆半径为R,则$|\overrightarrow{OA}|$=R,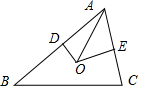
由图得,$\overrightarrow{OA}=\overrightarrow{OD}+\overrightarrow{DA}$,
则$\overrightarrow{AB}•\overrightarrow{OA}=\overrightarrow{AB}•(\overrightarrow{OD}+\overrightarrow{DA})$=$\overrightarrow{AB}•\overrightarrow{DA}$
=$\overrightarrow{AB}•(-\frac{1}{2}\overrightarrow{AB})$=$-\frac{1}{2}{\overrightarrow{AB}}^{2}$=$-\frac{1}{2}|{\overrightarrow{AB}|}^{2}$,
同理可得,$\overrightarrow{AC}•\overrightarrow{OA}=-\frac{1}{2}|\overrightarrow{AC}{|}^{2}$,
由$\frac{cosB}{sinC}\overrightarrow{AB}+\frac{cosC}{sinB}\overrightarrow{AC}=λ\overrightarrow{OA}$得,
$\frac{cosB}{sinC}\overrightarrow{AB}•\overrightarrow{OA}+\frac{cosC}{sinB}\overrightarrow{AC}•\overrightarrow{OA}=λ{\overrightarrow{OA}}^{2}$,
所以$-\frac{1}{2}•\frac{cosB}{sinC}|\overrightarrow{AB}{|}^{2}-\frac{1}{2}\frac{cosC}{sinB}|\overrightarrow{AC}{|}^{2}=λ{\overrightarrow{OA}}^{2}$,
则$cosB|\overrightarrow{AB}|\frac{|\overrightarrow{AB}|}{sinC}+cosC|\overrightarrow{AC}|\frac{|\overrightarrow{AC}|}{sinB}$=$-2λ|\overrightarrow{OA}{|}^{2}$,①
在△ABC中由正弦定理得:$\frac{|\overrightarrow{AB}|}{sinC}=\frac{|\overrightarrow{AC}|}{sinB}=2R$,
代入①得,$2RcosB|\overrightarrow{AB}|+2RcosC|\overrightarrow{AC}|=-2λ{R}^{2}$,
则$cosB|\overrightarrow{AB}|+cosC|\overrightarrow{AC}|=-λR$,②
由正弦定理得,$|\overrightarrow{AB}|=2RsinC$、$|\overrightarrow{AC}|=2RsinB$,
代入②得,2RsinCcosB+2RcosCsinB=-λR;
所以2sin(C+B)=-λ,即2sin$\frac{3π}{4}$=-λ,
解得λ=$-\sqrt{2}$,
故选D.
点评 本题考查了正弦定理,三角形外心的性质,向量数量积的运算,向量的线性运算,以及两角和的正弦公式的应用,考查化简、变形能力,分析问题、解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {3} | C. | {-2,3} | D. | .{-3,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
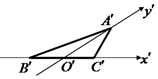 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com