
叙述并证明余弦定理.
解析 余弦定理:三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦之积的两倍.或:在△ABC中,a,b,c为A,B,C的对边,有a2=b2+c2-2bccos A,b2=c2+a2-2cacos B,c2=a2+b2-2abcos C,
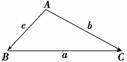 法一 如图(1),
法一 如图(1),
图(1)
a2=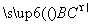 ·
·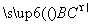
=(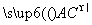 -
-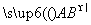 )·(
)·(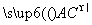 -
-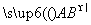 )
)
=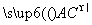 2-2
2-2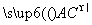 ·
·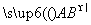 +
+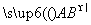 2
2
=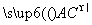 2-2|
2-2|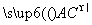 |·|
|·|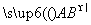 |cos A+
|cos A+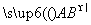 2
2
=b2-2bccos A+c2,即a2=b2+c2-2bccos A.
同理可证b2=c2+a2-2cacos B,c2=a2+b2-2abcos C.
 法二
法二
图(2)
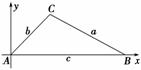
已知△ABC中A,B,C所对边分别为a,b,c,以A为原点,AB所在直线为x轴建立直角坐标系,如图(2)则C(bcos A,bsin A),B(c,0),
∴a2=|BC|2=(bcos A-c)2+(bsin A)2
=b2cos2A-2bccos A+c2+b2sin2A
=b2+c2-2bccos A.
同理可证b2=c2+a2-2cacos B,
c2=a2+b2-2abcos C.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
已知直线y=2与函数f(x)=2sin2ωx+2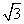 sinωxcosωx-1(ω>0)的图象的两个相邻交点之间的距离为π.
sinωxcosωx-1(ω>0)的图象的两个相邻交点之间的距离为π.
(1)求f(x)的解析式,并求出f(x)的单调递增区间;
(2)将函数f(x)的图象向左平移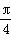 个单位长度得到函数g(x)的图象,求函数g(x)的最大值及g(x)取得最大值时x的取值集合.
个单位长度得到函数g(x)的图象,求函数g(x)的最大值及g(x)取得最大值时x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,为了测量某障碍物两侧A,B间的距离,给定下列四组数据,不能确定A,B间距离的是( ).
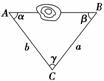
A.α,a,b B.α,β,a
C.a,b,γ D.α,β,b
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是________米.
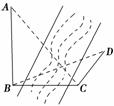
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com