
 矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.
矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.分析 (Ⅰ)只要证明AE⊥BC,AE⊥BE,即可证明AE⊥面BCE,而AE?面APE,从而可证平面PAE⊥平面BCE.
(Ⅱ)在直线AE上取点G,使得AG=2GE,连接PG,可证PCFG四点共面,由CF∥平面PAE,可证CF∥PG,可得PC和FG平行且相等,由PC=$\frac{1}{3}$CD,即可求得λ.
(Ⅲ)过P作AB的垂线,垂足为M,过M作BE的垂线,垂足为N,连接PN,可得PM⊥面ABE,又MN⊥BE,从而∠PNM为二面角P-EF-A的平面角,由余弦定理即可得解.
解答  解:(Ⅰ)∵AB=2AE,∠ABE=30°,
解:(Ⅰ)∵AB=2AE,∠ABE=30°,
∴AE⊥BE.…(2分)
∵ABCD为矩形,
∴BC⊥AB.
又∵面ABCD⊥面ABE,AB为面ABCD与面ABE的交线
∴BC⊥面ABE,∴BC⊥AE.…(3分)
∵AE⊥BC,AE⊥BE,而BC与BE相交于点B,
∴AE⊥面BCE,而AE?面APE,
∴平面PAE⊥平面BCE.…(4分)
(Ⅱ)在直线AE上取点G,使得AG=2GE,连接PG,
∵BF=2EF,∴FG∥$\frac{1}{3}$AB,
∴PCFG四点共面.…(6分)
∵CF∥平面PAE,而面FCPG∩面PAE=直线PG,
∴CF∥PG,∴四边形PCFG为平行四边形,
∴PC和FG平行且相等.…(8分)
∴PC=$\frac{1}{3}$CD,所以λ=2.…(9分)
(Ⅲ)过P作AB的垂线,垂足为M,过M作BE的垂线,垂足为N,连接PN…10分
∵面ABCD⊥面ABE,AB为面ABCD与面ABE的交线,
∴PM⊥面ABE,又因为MN⊥BE,
所以∠PNM为二面角P-EF-A的平面角…12分
可求得:PM=2,MN=$\frac{1}{2}$,PN=$\frac{\sqrt{17}}{2}$,
所以由余弦定理可得:cos∠PNM=$\frac{\sqrt{17}}{17}$…15分
点评 本题主要考查了直线与平面平行的判定,平面与平面垂直的判定,考查了二面角的平面角的求法,余弦定理的应用,考查了空间想象能力和转化思想,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),且抛物线x2=4y的焦点为椭圆的一个顶点,过P(0,2)的直线l分别与椭圆,抛物线交于不同的A,B,C,D四点.
已知平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-$\sqrt{3}$,0),且抛物线x2=4y的焦点为椭圆的一个顶点,过P(0,2)的直线l分别与椭圆,抛物线交于不同的A,B,C,D四点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
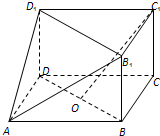 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
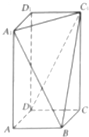 在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.
在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com