
分析 (1)利用抛物线的定义即可得出;
(2)当直线MN的斜率不存在时,直接求出即可.当直线MN的斜率存在时,且设为k(k≠0),则直线MN的方程为y=k(x-2),则直线PQ的方程为y=-$\frac{1}{k}$(x-2).设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4).分别与抛物线、椭圆方程联立可得根与系数的关系,再利用弦长公式、四边形的面积计算公式即可得出.
解答 解:(1)由椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1可知c2=9-5=4,则椭圆的右焦点为F(2,0).
由抛物线的定义可知,动圆的圆心轨迹为以F(2,0)为焦点,直线x=-2为准线的抛物线,
故轨迹C的方程为y2=8x.
(2)当直线MN的斜率不存在时,|MN|=8.此时PQ的长为椭圆的长轴长,PQ=6,
则SPMQN=$\frac{1}{2}\left|MN\right|$•|PQ|=$\frac{1}{2}$×8×6=24.
当直线MN的斜率存在时,且设为k(k≠0),则直线MN的方程为y=k(x-2),则直线PQ的方程为y=-$\frac{1}{k}$(x-2).
设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4).
由$\left\{\begin{array}{l}y=k(x-2)\\{y}^{2}=8x\end{array}\right.$消去y整理得k2x2-(4k2+8)x+4k2=0,
由抛物线定义可知|MN|=|MF|+|NF|=x1+2+x2+2=x1+x2+4=$\frac{4{k}^{2}+8}{{k}^{2}}$+4=8+$\frac{8}{{k}^{2}}$,
由$\left\{\begin{array}{l}y=-\frac{1}{k}(x-2)\\ \frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1\end{array}\right.$消去y整理得(5k2+9)x2-36x+36-45k2=0,
|PQ|=$\sqrt{1+(-\frac{1}{k})^{2}}\sqrt{({x}_{3}+{x}_{4})^{2}-4{x}_{3}{x}_{4}}$=$\sqrt{1+\frac{1}{{k}^{2}}}\sqrt{(\frac{36}{5{k}^{2}+9})^{2}-4\frac{36-45{k}^{2}}{5{k}^{2}+9}}$=$\frac{30(1+{k}^{2})}{5{k}^{2}+9}$,
则SPMQN=$\frac{1}{2}\left|MN\right|$•|PQ|=$\frac{1}{2}$•$\frac{8(1+{k}^{2})}{{k}^{2}}$•$\frac{30(1+{k}^{2})}{5{k}^{2}+9}$=120$\frac{(1+{k}^{2})^{2}}{5{k}^{4}+9{k}^{2}}$,
令1+k2=t,t>1,则SPMQN=$\frac{120{t}^{2}}{5{t}^{2}-t-4}$=$\frac{120}{5-\frac{1}{t}-\frac{4}{{t}^{2}}}$,
而5-$\frac{1}{t}$-$\frac{4}{{t}^{2}}$∈(0,5),则SPMQN∈(24,+∞).
综上可得:四边形PMQN面积的最小值为24.
点评 本题主要考查了抛物线的定义及其标准方程、直线与抛物线椭圆相交问题弦长问题、相互垂直的直线斜率之间的关系、四边形的面积计算公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | [2$\sqrt{2}$,+∞) | C. | (0,+∞) | D. | (2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.
矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
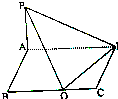 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com