
 设函数
设函数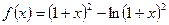 .
.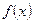 的单调区间;
的单调区间;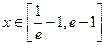 时,不等式
时,不等式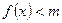 恒成立,求实数
恒成立,求实数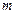 的取值范围;
的取值范围;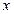 的方程
的方程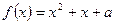 在
在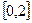 上恰有两个相异实根,求
上恰有两个相异实根,求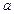 的取值范围.
的取值范围. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
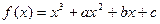 的图象过原点,且在x=1处取得极值,直线
的图象过原点,且在x=1处取得极值,直线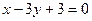 与曲线
与曲线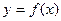 在原点处的切线互相垂直。
在原点处的切线互相垂直。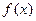 的解析式;
的解析式;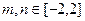 ,恒有
,恒有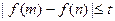 成立,求实数t的取值范围。
成立,求实数t的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
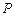 与日产量
与日产量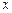 的函数关系是
的函数关系是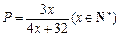 .
.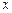 (件)的函数;
(件)的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
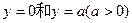 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为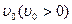 ,车速为
,车速为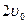 (水流速度忽略不计).
(水流速度忽略不计).
|
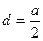 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
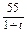 (单位:m/s)紧急刹车至停止.求:
(单位:m/s)紧急刹车至停止.求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
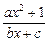 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com