Question

10．已知函数f（x）=|2x+2|-|2x-2|，x∈R．
（1）求不等式f（x）≤3的解集；
（2）若方程$\frac{f（x）}{2}+a=x$有三个实数根，求实数a的取值范围．

Answer 1

分析 （1）通过讨论x的范围，得到关于x的不等式组，求出不等式的解集即可；
（2）分离a，得到a=x+|x-1|-|x+1|，令h（x）=x+|x-1|-|x+1|，结合函数的图象求出a的范围即可．

解答 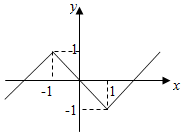解：（1）原不等式等价于$\left\{\begin{array}{l}x＜-1\\-4≤3\end{array}\right.$或$\left\{\begin{array}{l}-1≤x≤1\\ 4x≤3\end{array}\right.$或$\left\{\begin{array}{l}x＞1\\ 4≤3\end{array}\right.$，
解得：x＜-1或$-1≤x≤\frac{3}{4}$，
∴不等式f（x）≤3的解集为$（-∞，\frac{3}{4}]$．
（2）由方程$\frac{f（x）}{2}+a=x$可变形为a=x+|x-1|-|x+1|，
令$h（x）=x+|{x-1}|-|{x+1}|=\left\{\begin{array}{l}x+2，x＜-1\\-x，\;\;\;-1≤x≤1\\ x-2，x＞1\end{array}\right.$，
作出图象如下：

于是由题意可得-1＜a＜1．

点评 本题考查了解绝对值不等式问题，考查分类讨论思想以及数形结合思想，是一道中档题．