
【题目】若a>0,b>0,且 ![]() .
.
(I) 求a3+b3的最小值;
(Ⅱ)是否存在a,b,使得2a+3b=6?并说明理由.
【答案】【解答】解:(Ⅰ)∵a>0,b>0,且 ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]() ≥2
≥2 ![]() ,∴ab≥2,
,∴ab≥2,
当且仅当a=b= ![]() 时取等号.
时取等号.
∵a3+b3 ≥2 ![]() ≥2
≥2 ![]() =4
=4 ![]() ,当且仅当a=b=
,当且仅当a=b= ![]() 时取等号,
时取等号,
∴a3+b3的最小值为4 ![]() .
.
(Ⅱ)∵2a+3b≥2 ![]() =2
=2 ![]() ,当且仅当2a=3b时,取等号.
,当且仅当2a=3b时,取等号.
而由(1)可知,2 ![]() ≥2
≥2 ![]() =4
=4 ![]() >6,
>6,
故不存在a,b,使得2a+3b=6成立.
【解析】(1)两次连续代入![]() 公式,注意“=”成立条件是:当且仅当a=b.
公式,注意“=”成立条件是:当且仅当a=b.
(2)同样代入![]() 公式,此时“=”成立的条件是2a=3b,与题目a=b不同,故不成立。
公式,此时“=”成立的条件是2a=3b,与题目a=b不同,故不成立。
【考点精析】利用基本不等式对题目进行判断即可得到答案,需要熟知基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】给出关于双曲线的三个命题:
①双曲线 ![]() ﹣
﹣ ![]() =1的渐近线方程是y=±
=1的渐近线方程是y=± ![]() x;
x;
②若点(2,3)在焦距为4的双曲线 ![]() ﹣
﹣ ![]() =1上,则此双曲线的离心率e=2;
=1上,则此双曲线的离心率e=2;
③若点F,B分别是双曲线 ![]() ﹣
﹣ ![]() =1的一个焦点和虚轴的一个端点,则线段FB的中点一定不在此双曲线的渐近线上.
=1的一个焦点和虚轴的一个端点,则线段FB的中点一定不在此双曲线的渐近线上.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,四边形ABCD的各顶点均在椭圆E上,且对角线AC,BD均过坐标原点O,点D(2,1),AC,BD的斜率之积为
,四边形ABCD的各顶点均在椭圆E上,且对角线AC,BD均过坐标原点O,点D(2,1),AC,BD的斜率之积为 ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过D作直线l平行于AC.若直线l′平行于BD,且与椭圆E交于不同的两点M.N,与直线l交于点P.
⑴证明:直线l与椭圆E有且只有一个公共点;
⑵证明:存在常数λ,使得|PD|2=λ|PM||PN|,并求出λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+bx+1的图象在x=1处的切线l过点(
ax2+bx+1的图象在x=1处的切线l过点( ![]() ,
, ![]() ).
).
(1)若函数g(x)=f(x)﹣(a﹣1)x(a>0),求g(x)最大值(用a表示);
(2)若a=﹣4,f(x1)+f(x2)+x1+x2+3x1x2=2,证明:x1+x2≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,首项 ![]() ,前n项和为Sn , 且
,前n项和为Sn , 且 ![]()
(1)求数列{an}的通项
(2)如果bn=3(n+1)×2nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产每一吨产品所需的劳动力、煤和电如下表:
产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦时) |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦时,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若图,在三棱柱 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,且
,且 ![]() 和
和 ![]() 均为正三角形.
均为正三角形.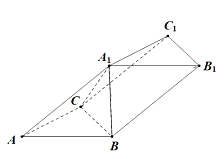
(1)在 ![]() 上找一点
上找一点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并说明理由.
,并说明理由.
(2)若 ![]() 的面积为
的面积为 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 是
是 ![]() 上的动点.现将矩形
上的动点.现将矩形 ![]() 沿着对角线
沿着对角线 ![]() 折成二面角
折成二面角 ![]() ,使得
,使得 ![]() .
.
(Ⅰ)求证:当 ![]() 时,
时, ![]() ;
;
(Ⅱ)试求 ![]() 的长,使得二面角
的长,使得二面角 ![]() 的大小为
的大小为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com