
分析 (Ⅰ)由题意知f(x)的定义域为(0,+∞),且f′(x)=$\frac{1}{x}$+$\frac{a}{{x}^{2}}$=$\frac{x+a}{{x}^{2}}$,由此得到f(x)在(0,+∞)上是单调递增函数.
(Ⅱ)由f′(x)=$\frac{x+a}{{x}^{2}}$,根据a≥-1,a≤-e,-e<a<-1,进行分类讨论,利用导数性质能求出a的值.
(Ⅲ)推导出lnx-$\frac{1}{2}λ$(x-$\frac{1}{x}$)≤0,令$G(x)=lnx-\frac{1}{2}λ(x-\frac{1}{x}),G'(x)=\frac{{-λ{x^2}+2x-λ}}{{2{x^2}}}$,要所λ≤-1,-1<λ<0,λ=0,0<λ<1,λ≥1进行分类讨论,利用导数性质能求出λ的最小值.
解答 解:(Ⅰ)∵f(x)=lnx-$\frac{a}{x}$,
∴由题意知f(x)的定义域为(0,+∞) …(1分)
且f′(x)=$\frac{1}{x}$+$\frac{a}{{x}^{2}}$=$\frac{x+a}{{x}^{2}}$.…(3分)
∵a>0,∴f′(x)>0,
故f(x)在(0,+∞)上是单调递增函数.…(5分)
(Ⅱ)由(1)可知,f′(x)=$\frac{x+a}{{x}^{2}}$.
①若a≥-1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,
此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=-a=$\frac{3}{2}$,∴a=-$\frac{3}{2}$(舍去).
②若a≤-e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,
此时f(x)在[1,e]上为减函数,
∴f(x)min=f(e)=1-$\frac{a}{e}$=$\frac{3}{2}$,∴a=-$\frac{e}{2}$(舍去).
③若-e<a<-1,令f′(x)=0得x=-a,
当1<x<-a时,f′(x)<0,∴f(x)在(1,-a)上为减函数;
当-a<x<e时,f′(x)>0,∴f(x)在(-a,e)上为增函数,
∴f(x)min=f(-a)=ln(-a)+1=$\frac{3}{2}$,∴a=-$\sqrt{e}$.
综上所述,a=-$\sqrt{e}$.
(Ⅲ)∵xf(x)≤λ[g(x)+x],∴$xlnx≤λ[\frac{1}{2}(x-1)^{2}-1+x]$,
∴xlnx≤λ($\frac{1}{2}{x}^{2}-\frac{1}{2}$),∴lnx-$\frac{1}{2}λ$(x-$\frac{1}{x}$)≤0,
令 $G(x)=lnx-\frac{1}{2}λ(x-\frac{1}{x}),G'(x)=\frac{{-λ{x^2}+2x-λ}}{{2{x^2}}}$,
当λ≤-1时,△=4-4(-λ)(-λ)≤0,故恒有-λx2+2x-λ≥0,
则G′(x)≥0恒成立,故G(x)在区间[1,+∞)单调递增,
∴G(x)≥G(1)=0,这与条件矛盾;
当-1<λ<0时,x=-$\frac{2}{2(-λ)}=\frac{1}{λ}<0$,
故有y=-λx2+2x-λ在区间[1,+∞)上单调递增,
故有-λx2+2x-λ>2-2λ>0,则G′(x)≥0恒成立,
故G(x)在区间[1,+∞)上恒单调递增,
∴G(x)≥G(1)=0,这与条件矛盾;
当λ=0时,G′(x)=$\frac{2x}{2{x}^{2}}$>0,故G(x)在区间[1,+∞)上单调递增,
∴G(x)≥G(1),这与条件矛盾;
当0<λ<1时,设-λx2+2x-λ=0的两根为x1,x2,且x1<x2,
∵${x}_{1}+{x}_{2}=\frac{2}{λ}>2,{x}_{1}{x}_{2}=1$,
∴0<x1<1<x2,∴x∈(1,x2)时,-λx2+2x-λ>0,
故函数G(x)在区间(1,x2)上单调递增,
∴G(x2)≥G(1)=0,这与条件矛盾;
当λ≥1时,△=4-4(-λ)(-λ)≤0,故恒有-λx2+2x-λ≤0,
∴G′(x)≤0恒成立,故G(x)在区间[1,+∞)上单调递减,
∴G(x)≤G(1)=0,命题成立.
综上所述λ≥1,所以λ的最小值为1.…(12分)
点评 本题考查函数单调性质的判断,考查实数值、导数性质、构造法、函数单调性等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想,是中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
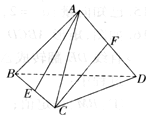 如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )
如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({3,3+2\sqrt{2}})$ | B. | $({3,3+2\sqrt{2}}]$ | C. | (1,3) | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 56 | C. | 68 | D. | 78 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com