
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)
)∪(1,+∞)
B.( ![]() ,1)
,1)
C.( ![]() )
)
D.(﹣∞,﹣ ![]() ,)
,) ![]()
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有
①刻画一组数据集中趋势的统计量有极差、方差、标准差等;刻画一组数据离散程度统计量有平均数、中位数、众数等.
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大.
③有10个阄,其中一个代表奖品,10个人按顺序依次抓阄来决定奖品的归属,则摸奖的顺序对中奖率没有影响.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x﹣my+3=0和圆C:x2+y2﹣6x+5=0
(1)当直线l与圆C相切时,求实数m的值;
(2)当直线l与圆C相交,且所得弦长为 ![]() 时,求实数m的值.
时,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是 ![]() .
. 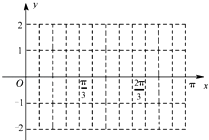
(1)求φ;
(2)在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(3)求函数f(x)≥1(x∈R)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有体育特长生25人,美术特长生35人,音乐特长生40人.用分层抽样的方法从中抽取40人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
A.8,14,18
B.9,13,18
C.10,14,16
D.9,14,17
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,做了一次相关调查,其中部分数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
(1)若吸烟不患肺癌的有![]() 人,现从患肺癌的人中用分层抽样的方法抽取
人,现从患肺癌的人中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行调查,求这两人都是吸烟患肺癌的概率;
人进行调查,求这两人都是吸烟患肺癌的概率;
(2)若研究得到在犯错误概率不超过![]() 的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
附: 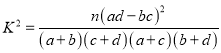 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在静水中游泳,速度为4![]() 公里/小时,他在水流速度为4公里/小时的河中游泳.
公里/小时,他在水流速度为4公里/小时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com