
分析 平面AB1D1与正方体的12条棱所成的角都相等,且平面AB1D1与正方体的6个面所成较小的二面角都相等;直线AC1与正方体的12条棱所成的角都相等,且直线AC1与正方体的6个面所成的角都相等.
解答  解:如图,连接AB1D1,则A1-AB1D1为正三棱锥,则A1B1、A1D1、A1A与平面AB1D1所成角相等,
解:如图,连接AB1D1,则A1-AB1D1为正三棱锥,则A1B1、A1D1、A1A与平面AB1D1所成角相等,
则存在一个平面AB1D1与正方体的12条棱所成的角都相等,故①正确;
正三棱锥A1-AB1D1的三个侧面与底面AB1D1所成角相等,
则存在一个平面AB1D1与正方体的6个面所成较小的二面角都相等,故②正确;
③存在一条直线AC1与正方体的12条棱所成的角都相等,故③正确;
④存在一条直线AC1与正方体的6个面所成的角都相等,故④正确.
故答案为:①②③④.
点评 本题考查命题真假的判断与应用,考查空间想象能力和思维能力,注意正方体结构特征的合理运用,是中档题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于点($\frac{5π}{12}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
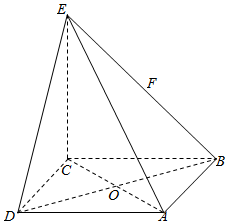 在四棱锥E-ABCD中,底面ABCD是边长为1的正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是边长为1的正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,某流动海洋观测船开始位于灯塔B的北偏东θ(0<θ<$\frac{π}{2}$)方向,且满足2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投浮标,使得C点于A点的距离为4$\sqrt{3}$km,则该观测船行驶的最远航程为8km.
如图,某流动海洋观测船开始位于灯塔B的北偏东θ(0<θ<$\frac{π}{2}$)方向,且满足2sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投浮标,使得C点于A点的距离为4$\sqrt{3}$km,则该观测船行驶的最远航程为8km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com