练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a，b，c∈（0，1），则对于（1﹣a）b，（1﹣b）c，（1﹣c）a说法正确的是（ ）

    A.不能都大于 B.都大于

    C.都小于 D.至少有一个大于

     

    A

    【解析】

    试题分析：首先根据题意，通过反证法得出结论．

    【解析】
    假设（1﹣a）b，（1﹣b）c，（1﹣c）a中都大于

    即（1﹣a）b＞，（1﹣b）c＞，（1﹣c）a＞，

    即＞①＞②＞③

    ①②③相加：++＞

    由基本不等式++≤=

    矛盾所以假设不成立，∴（1﹣a）b，（1﹣b）c，（1﹣c）a中至少有一个不大于．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷（解析版） 题型：解答题

    若a1≤a2≤…≤an，而b1≥b2≥…≥bn或a1≥a2≥…≥an而b1≤b2≤…≤bn，证明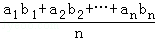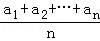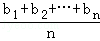：≤（）•（）．当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：

    ①A+B+C=90°+90°+C＞180°，这与三角形内角和为180°相矛盾，A=B=90°不成立；

    ②所以一个三角形中不能有两个直角；

    ③假设三角形的三个内角A、B、C中有两个直角，不妨设A=B=90°，

    正确顺序的序号为（ ）

    A.①②③ B.①③② C.②③① D.③①②

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（ ）

    A.假设三内角都不大于60度

    B.假设三内角都大于60度

    C.假设三内角至多有一个大于60度

    D.假设三内角至多有两个大于60度

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：选择题

    要证，只需证+1，即需证，即需证，即证35＞11，因为35＞11显然成立，所以原不等式成立．以上证明运用了（ ）

    A.比较法 B.综合法 C.分析法 D.反证法

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.1比较法练习卷（解析版） 题型：填空题

    对任意的实数x，不等式x+|x﹣1|＞m恒成立，则实数m的取值范围是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.1比较法练习卷（解析版） 题型：填空题

    （2010•江苏模拟）对于任意的x∈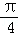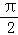（，），不等式psin4x+cos6x≤2sin4x恒成立，则实数p的取值范围为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：填空题

    （2014•重庆模拟）不等式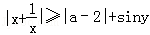对一切非零实数x，y均成立，则实数a的范围为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.1不等式练习卷（解析版） 题型：选择题

    （2014•淄博一模）设a＞1，b＞0，若a+b=2，则的最小值为（ ）

    A.3+2 B.6 C.4 D.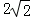

     

    查看答案和解析>>

    同步练习册答案