
| A. | 对分类变量x与y的随机变量k2的观测值k来说,k越小,判断“x与y有关系”的把握程度越大 | |
| B. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于0 | |
| C. | 若数据x1,x2,x3,…,xn的方差为1,则2x1,2x2,2x3,…,2xn的方差为2 | |
| D. | 在回归分析中,可用相关指数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好. |
分析 对四个选项分别进行判断,即可得出结论.
解答 解:A,对分类变量x与y的随机变量K2的观测值k来说,k越大,判断“x与y有关系”的把握程度越大,故错误;
B,根据|r|越趋近于1,两个随机变量的相关性越强,故错误;
C,数据x1,x2,x3,…,xn和2x1,2x2,2x3,…,2xn的数据满足Y=2X,则方程满足DY=4DX,
若数据x1,x2,x3,…,xn的方差为1,则2x1,2x2,2x3,…,2xn的方差为4正确,故错误;
D,用相关指数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好,故正确.
故选D.
点评 本题主要考查回归分析,属于基础题,解答此题的关键是理解对于拟合效果好坏的几个量的大小反映的拟合效果的好坏,以及对于某组数据可以采用几种不同的回归方程进行分析,可以通过比较相关系数的值选择较大的模型作为这组数据的模型.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
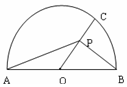 如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )
如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )| A. | 2 | B. | -1 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com