
分析 由题意知本题是一个几何概型,试验发生包含的所有事件对应的集合是Ω={(x,y)|0<x<5,0<y<5}做出集合对应的面积是边长为5的正方形的面积,写出满足条件的事件对应的集合和面积,根据面积之比得到概率
解答  解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
∵试验发生包含的所有事件对应的集合是Ω={(x,y)|0<x<5,0<y<5}
集合对应的面积是边长为5的正方形的面积s=25,
而满足条件的事件对应的集合是A═{(x,y)|0<x<5,0<y<5,|x-y|≤1}
得到sA=9
∴两人能够会面的概率是$\frac{9}{25}$;
故答案为:$\frac{9}{25}$.
点评 本题考查了几何概型;解答本题的难点是把时间分别用x,y坐标来表示,从而把时间长度这样的一维问题转化为平面图形的二维面积问题,转化成面积型的几何概型问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}$(1-4-n) | B. | $\frac{32}{3}$(1-2-n) | C. | 16(1-4-n) | D. | 16(1-2-n) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a+1)>f(2-b) | B. | f(a+1)=f(2-b) | C. | f(a+1)<f(2-b) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
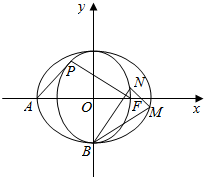 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com