
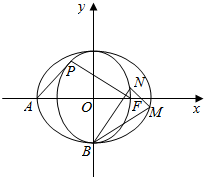
 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.分析 (1)利用面积公式求得点的坐标,进而证明结论成立.
(2)利用两条直线分别与圆锥曲线联立求得直线斜率,得到所求直线方程,得出定点.
解答 解:(1)证明:设曲线C1上的点P(x0,y0),且x0<0,y0>0,
由题意A($-\sqrt{2},0$),F(1,0),∵△APF的面积为$\frac{1}{2}+\frac{\sqrt{2}}{4}$,
∴${S}_{△APF}=\frac{1}{2}AF\\;y$$y=\frac{1}{2}(1+\sqrt{2}){y}_{0}=\frac{1}{2}+\frac{\sqrt{2}}{4}$,解得${y}_{0}=\frac{\sqrt{2}}{2},{x}_{0}=-\frac{\sqrt{2}}{2}$,即$P(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$
∴$\overrightarrow{AP}•\overrightarrow{OP}=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})•(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})=0$,∴AP⊥OP
(2)设直线BM的斜率为k,则直线BN的斜率为2k,又两直线都过点B(0,-1),
∴直线BM的方程为y=kx-1,直线BN的方程为y=2kx-1.
由$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,得(1+2k2)x2-4kx=0
解得${x}_{M}=\frac{4k}{1+2{k}^{2}},{y}_{M}=k\frac{4k}{2{k}^{2}+1}-1=\frac{2{k}^{2}-1}{2{k}^{2}+1}$,即M($\frac{4k}{2{k}^{2}+1},\frac{2{k}^{2}-1}{2{k}^{2}+1}$)
$\left\{\begin{array}{l}{y=2kx-1}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,得(1+4k2)x2-4kx=0
解得,${x}_{N}=\frac{4k}{4{k}^{2}+1},{y}_{N}=2k×\frac{4k}{4{k}^{2}+1}-1$=$\frac{4{k}^{2}-1}{4{k}^{2}+1}$,即N($\frac{4k}{4{k}^{2}+1},\frac{4{k}^{2}-1}{4{k}^{2}+1}$)
直线MN的斜率kMN=$\frac{\frac{4{k}^{2}-1}{4k2+1}-\frac{2{k}^{2}-1}{2{k}^{2}+1}}{\frac{4k}{4{k}^{2}+1}-\frac{4k}{2{k}^{2}+1}}$=$\frac{(4{k}^{2}-1)(2{k}^{2}+1)-(4{k}^{2}+1)(2{k}^{2}-1)}{4k(2{k}^{2}+1)-4k(4{k}^{2}+1)}$=$-\frac{1}{2k}$
∴直线MN的方程为$y-\frac{2{k}^{2}-1}{2{k}^{2}+1}=-\frac{1}{2k}(x-\frac{4k}{2{k}^{2}+1})$,
整理得,$y=-\frac{1}{2k}x+1$,∴直线MN恒过定点(0,1).
点评 本题主要考查直线与圆锥曲线的综合问题,在高考中属于较难题目.常考题型,难度较大.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | [-1,3] | C. | [3,+∞) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.
第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com