
分析 (1)通过直线l的方程可得D、E坐标,将y=2x-4代入y2=4x可得点A、B坐标,利用$\overrightarrow{EA}={λ_1}\overrightarrow{AD}$、$\overrightarrow{EB}={λ_2}\overrightarrow{BD}$,计算即可;
(2)通过联立x=my+1(m>1)与$\frac{x^2}{2}+{y^2}$=1,利用韦达定理、$\overrightarrow{EA}={λ_1}\overrightarrow{AD}$、$\overrightarrow{EB}={λ_2}\overrightarrow{BD}$,计算即得结论;
(3)通过设直线l的方程并与双曲线C方程联立,利用韦达定理、$\overrightarrow{EA}={λ_1}\overrightarrow{AD}$,$\overrightarrow{EB}={λ_2}\overrightarrow{BD}$,计算即可.
解答 解:(1)将y=2x-4代入y2=4x,求得点A(1,-2),B(4,4),
又∵D(2,0),E(0,-4),且$\overrightarrow{EA}={λ_1}\overrightarrow{AD}$,
∴(1,2)=λ1(1,2)=(λ1,2λ1),即λ1=1,
同理由$\overrightarrow{EB}={λ_2}\overrightarrow{BD}$,可得λ2=-2,
∴λ1+λ2=-1;
(2)联立x=my+1(m>1)与$\frac{x^2}{2}+{y^2}$=1,
消去x可得:(2+m2)y2+2my-1=0,
由韦达定理可得:y1+y2=-$\frac{2m}{2+{m}^{2}}$,y1y2=-$\frac{1}{2+{m}^{2}}$,
∵D(1,0),E(0,-$\frac{1}{m}$),且$\overrightarrow{EA}={λ_1}\overrightarrow{AD}$,
∴y1+$\frac{1}{m}$=-λ1y1,∴λ1=-(1+$\frac{1}{m}•\frac{1}{{y}_{1}}$),
同理由$\overrightarrow{EB}={λ_2}\overrightarrow{BD}$,可得y2+$\frac{1}{m}$=-λ2y2,∴λ2=-(1+$\frac{1}{m}•\frac{1}{{y}_{2}}$),
∴λ1+λ2=-(1+$\frac{1}{m}•\frac{1}{{y}_{1}}$)-(1+$\frac{1}{m}•\frac{1}{{y}_{2}}$)=-2-$\frac{1}{m}•\frac{{y}_{1}+{y}_{2}}{{y}_{1}{y}_{2}}$=-2-$\frac{1}{m}•2m$=-4,
∴$\frac{1}{λ_1}+\frac{1}{λ_2}$=-$\frac{4}{{λ}_{1}{λ}_{2}}$=$\frac{4}{{{λ}_{1}}^{2}+4{λ}_{1}}$=$\frac{4}{(2+{λ}_{2})^{2}-4}$,
∵m>1,∴点A在椭圆上位于第三象限的部分上运动,
由分点的性质可得λ1∈($\sqrt{2}-2$,0),
∴$\frac{1}{λ_1}+\frac{1}{λ_2}$∈(-∞,-2);
(3)设直线l的方程为:x=my+t,代入双曲线C方程,
消去x得:(-3+m2)y2+2mty+(t2-3)=0,
由韦达定理可得:y1+y2=-$\frac{2mt}{{m}^{2}-3}$,y1y2=-$\frac{{t}^{2}-3}{{m}^{2}-3}$,∴$\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{2}}$=-$\frac{2mt}{{t}^{2}-3}$,
由$\overrightarrow{EA}={λ_1}\overrightarrow{AD}$,$\overrightarrow{EB}={λ_2}\overrightarrow{BD}$可得:-(λ1+λ2)=2+$\frac{t}{m}$•($\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{2}}$),
∵λ1+λ2=6,∴2+$\frac{t}{m}$•(-$\frac{2mt}{{t}^{2}-3}$)=-6,解得t=±2,
∴点D(±2,0);
当直线l与x轴重合时,λ1=-$\frac{a}{t+a}$,λ2=$\frac{a}{t-a}$或者λ1=$\frac{a}{t-a}$,λ2=-$\frac{a}{t+a}$,
∴都有λ1+λ2=$\frac{2{a}^{2}}{{t}^{2}-{a}^{2}}$=6也满足要求,
∴在x轴上存在定点D(±2,0).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(a+1)>f(2-b) | B. | f(a+1)=f(2-b) | C. | f(a+1)<f(2-b) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
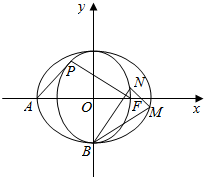 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
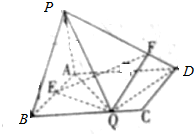 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com