
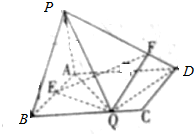
 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.分析 (1)以A为原点,边AB,AD,AP所在直线分别为x,y,z轴,建立空间直角坐标系,根据已知条件求出点A,Q,E,F的坐标,求数量积等于0即可;
(2)设F(0,y,z),根据条件$\overrightarrow{PF}$=λ$\overrightarrow{PD}$便可求得F(0,2λ,1-λ),取AQ中点M,容易判断出BM为平面PAQ的一个法向量.求出平面EFQ的法向量,利用平面PAQ与平面EFQ所成锐二面角的大小为60°,可建立关于λ的方程,解方程即得λ的值.
解答 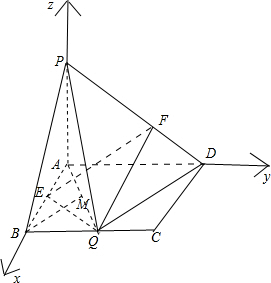 (1)证明:由题意,仅存在唯一一点Q,使得PQ⊥QD,则a=2,如图,以A为原点,直线AB,AD,AP分别为x,y,z轴建立空间直角坐标系,则:
(1)证明:由题意,仅存在唯一一点Q,使得PQ⊥QD,则a=2,如图,以A为原点,直线AB,AD,AP分别为x,y,z轴建立空间直角坐标系,则:
A(0,0,0),E($\frac{1}{2}$,0,0),Q(1,1,0),P(0,0,1),D(0,2,0),B(1,0,0);
设F(0,y,z),∴$\overrightarrow{PF}$=(0,y,z-1),$\overrightarrow{PD}$=(0,2,-1)
∵$\overrightarrow{PF}$=$\frac{1}{4}$$\overrightarrow{PD}$
∴(0,y,z-1)=$\frac{1}{4}$(0,2,-1);
∴y=$\frac{1}{2}$,z=$\frac{3}{4}$,
∴F(0,$\frac{1}{2}$,$\frac{3}{4}$),
∴$\overrightarrow{EF}$=(-$\frac{1}{2}$,$\frac{1}{2}$,$\frac{3}{4}$),
∵$\overrightarrow{AQ}$=(1,1,0),
∴$\overrightarrow{AQ}$•$\overrightarrow{EF}$=0,
∴AQ⊥EF;
(2)设F(0,y,z),$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,
∴(0,y,z-1)=λ(0,2,-1);
∴y=2λ,z=1-λ,
∴F(0,2λ,1-λ);
取AQ的中点为M,连接BM,则M($\frac{1}{2}$,$\frac{1}{2}$,0)
∵AB=BQ;
∴BM⊥AQ;
又PA⊥平面ABCD,BM?平面ABCD;
∴PA⊥BM,即BM⊥PA,PA∩AQ=A;
∴BM⊥平面PAQ;
∴$\overrightarrow{BM}$=(-($\frac{1}{2}$,$\frac{1}{2}$,0)为平面PAQ的一个法向量;
设平面EFQ的法向量为$\overrightarrow{n}$=(x,y,z)
则$\left\{\begin{array}{l}{-\frac{1}{2}x+2λy+(1-λ)z=0}\\{\frac{1}{2}x+y=0}\end{array}\right.$
∴$\overrightarrow{n}$=(-2,1,$\frac{1+2λ}{λ-1}$)
∵平面PAQ与平面EFQ所成锐二面角的大小为60°
∴cos60°=$\frac{1+\frac{1}{2}}{\sqrt{5+(\frac{1+2λ}{λ-1})^{2}}•\sqrt{\frac{1}{2}}}$
∴解得λ=$\frac{5-\sqrt{13}}{3}$,或λ=$\frac{5+\sqrt{13}}{3}$(舍去).
即λ=$\frac{5-\sqrt{13}}{3}$.
点评 考查建立空间直角坐标系,利用空间向量证明空间异面直线垂直,解决空间角的方法,以及两非零向量垂直的充要条件,线面垂直的性质,线面垂直的判定定理,平面法向量的概念,向量数量积的坐标运算,向量夹角余弦的坐标公式,平面法向量的夹角和平面二面角的平面角度大小的关系.


科目:高中数学 来源: 题型:解答题
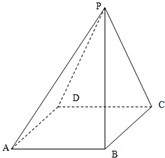 如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.
如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
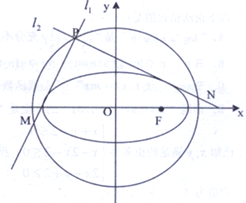 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com