
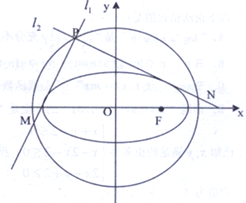
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$分析 (1)利用椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$,求出c,a,可得b,即可求椭圆C的离心率及其标准方程;
(Ⅱ)分类讨论:l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,无论两条直线中的斜率是否存在,都有l1,l2垂直.即可得出线段MN为准圆x2+y2=4的直径.
解答 解:(1)由题意,a=$\sqrt{3}$,c=$\sqrt{2}$,
∴b=1,
∴e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,椭圆的方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$;
(2)证明:①当直线l1,l2中有一条斜率不存在时,不妨设直线l1斜率不存在,
则l1:x=±$\sqrt{3}$,
当l1:x=$\sqrt{3}$时,l1与准圆交于点($\sqrt{3}$,1),($\sqrt{3}$,-1),
此时l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证当l1:x=-$\sqrt{3}$时,直线l1,l2垂直.
②当l1,l2斜率存在时,设点P(x0,y0),其中x02+y02=4.
设经过点P(x0,y0)与椭圆相切的直线为y=t(x-x0)+y0,
代入椭圆方程得(1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.
由△=0化简整理得(3-x02)t2+2x0y0t+1-y02=0,
∵x02+y02=4,∴有(3-x02)t2+2x0y0t+x02-3=0.
设l1,l2的斜率分别为t1,t2,
∵l1,l2与椭圆相切,
∴t1,t2满足上述方程(3-x02)t2+2x0y0t+x02-3=0.,
∴t1•t2=-1,即l1,l2垂直.
综合①②知:∵l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直.
∴线段MN为准圆x2+y2=4的直径,|MN|=4,
∴线段MN的长为定值.
点评 本题考查了椭圆的标准方程及其性质、新定义、直线与椭圆相切?△=0、直线垂直与斜率的关系、分类讨论等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b>0,则$\frac{1}{a}<\frac{1}{b}$”的逆命题是真命题 | |
| B. | 命题p:?x∈R,2x>0,则¬p:?x0∈R,2x0<0 | |
| C. | “a>1,b>1”是“ab>1”成立的充分条件 | |
| D. | “a>b”是“a2>b2”成立的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
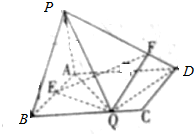 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com