
分析 (1)利用函数在点(1,f(1))处的切线与直线y=2x+1平行,得到f'(1)=2,然后利用导数确定a,b满足的关系式.
(2)构造函数g(x)=f(x)-2lnx=ax+$\frac{a-2}{x}$+2-2a-2lnx,x∈[1,+∞),利用导数求函数的最值即可.
(3)取a=1得x-$\frac{1}{x}$≥2lnx令x=$\frac{2n+1}{2n-1}$>1得$\frac{2n+1}{2n-1}$-$\frac{2n-1}{2n+1}$>2ln$\frac{2n+1}{2n-1}$,即$\frac{1}{2n-1}$>$\frac{1}{2}$ln$\frac{2n+1}{2n-1}$+$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),上式中n=1,2,3,…,n,然后n个不等式相加得结论.
解答 (1)解:函数的导数为f′(x)=a-$\frac{b}{{x}^{2}}$,
因为f(x)=ax+$\frac{b}{x}$+2-2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
所以f'(1)=2,即f'(1)=a-b=2,所以b=a-2.
(2)解:因为b=a-2,所以f(x)=ax+$\frac{a-2}{x}$+2-2a,
若f(x)≥2lnx,则f(x)-2lnx≥0,
设g(x)=f(x)-2lnx=ax+$\frac{a-2}{x}$+2-2a-2lnx,x∈[1,+∞).
则g(1)=0,g′(x)=$\frac{a(x-1)(x-\frac{2-a}{a})}{{x}^{2}}$,
①当0<a<1时,$\frac{2-a}{a}$>1,若1<x<$\frac{2-a}{a}$,则g'(x)<0,此时g(x)在[1,+∞)上单调递减,所以g(x)<g(1)=0,即f(x)≥2lnx在[1,+∞)不恒成立.
②若a≥1,$\frac{2-a}{a}$≤1,当x>1时,g'(x)>0,g(x)在[1,+∞)上单调递增,又g(1)=0,
所以此时f(x)≥2lnx.
综上所述,所求a的取值范围是[1,+∞).
(3)证明:由(2)知当a≥1时,f(x)≥2lnx在[1,+∞)上恒成立.
取a=1得x-$\frac{1}{x}$≥2lnx
令x=$\frac{2n+1}{2n-1}$>1得$\frac{2n+1}{2n-1}$-$\frac{2n-1}{2n+1}$>2ln$\frac{2n+1}{2n-1}$,
即$\frac{1}{2n-1}$>$\frac{1}{2}$ln$\frac{2n+1}{2n-1}$+$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
上式中n=1,2,3,…,n,然后n个不等式相加得1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2n-1}$>$\frac{1}{2}$ln(2n+1)+$\frac{n}{2n+1}$(n∈N*).
点评 本题主要考查导数的几何意义,以及利用导数研究函数的性质,考查学生的运算能力.综合性较强.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
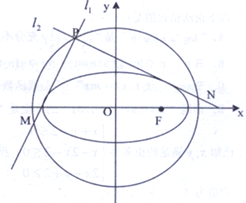 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值7 | B. | 有最大值-7 | C. | 有最小值7 | D. | 有最小值-7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\sqrt{3}π$ | D. | $2\sqrt{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com