
| API | [0��50] | ��50��100] | ��100��150] | ��150��200] | ��200��250] | ��250��+�ޣ� |
| ���� | 6 | 12 | 22 | 30 | 14 | 16 |
���� ��1�����ݷֲ�����ó���������֡����족�ĸ��ʣ�
��2��ȷ��X�����п���ȡֵΪ45��70��95��120�����ö���ֵĸ���֪ʶ���$P��X=70��=C_3^1��0.4��{��0.6��^2}=0.432$��$P��X=95��=C_3^2��{��0.4��^2}��0.6=0.288$��P��X=120��=��0.4��3=0.064���������÷ֲ������E��X����D��X����
��� �⣺��1������ͳ�����ݳ��ֺ���ĸ���Ϊ0.4��
������������֡����족�ĸ���Ϊ0.4��0.4=0.16��
��2��X�����п���ȡֵΪ45��70��95��120
��P��X=45��=��0.6��3=0.216
$P��X=70��=C_3^1��0.4��{��0.6��^2}=0.432$
$P��X=95��=C_3^2��{��0.4��^2}��0.6=0.288$
P��X=120��=��0.4��3=0.064
| X | 45 | 70 | 95 | 120 |
| P | 0.216 | 0.432 | 0.288 | 0.064 |
���� ��С����Ҫ����ͳ������ʵ����֪ʶ�����а������ʵ�����ɢ�������������ѧ�����Լ����������Ҫ����ѧ�������ݴ����������������������


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2012 | B�� | 2013 | C�� | 2014 | D�� | 2015 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
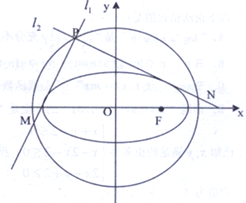 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����һ������F��$\sqrt{2}$��0��������ϵ�һ���˵㵽F�ľ���Ϊ$\sqrt{3}$
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����һ������F��$\sqrt{2}$��0��������ϵ�һ���˵㵽F�ľ���Ϊ$\sqrt{3}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | 8 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com