
分析 (1)由条件利用余弦定理求得cosA的值,可得A的值.
(2)根据sinAsinB=$\frac{1+cosC}{2}$,利用两角和差的余弦公式花简求得cos(A-B)=1,可得A=B=$\frac{π}{6}$,可得C的值,从而求得△ABC的面积S=$\frac{1}{2}$ab•sinC 的值.
解答 解:(1)△ABC中,∵a2=(b-c)•22+(2-$\sqrt{3}$)bc,∴b2+c2-a2=$\sqrt{3}$bc,
∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=$\frac{\sqrt{3}}{2}$,∴A=$\frac{π}{6}$.
(2)∵sinAsinB=$\frac{1+cosC}{2}$,∴2sinAsinB=1+cosC=1-cos(A+B)=1-(cosAcosB-sinAsinB),
化简可得cos(A-B)=1,∴A-B=0,即A=B=$\frac{π}{6}$,C=$\frac{2π}{3}$.
再根据 a=4,可得△ABC的面积S=$\frac{1}{2}$ab•sinC=4$\sqrt{3}$.
点评 本题主要考查正弦定理、余弦定理的应用,两角和差的余弦公式,根据三角函数的值求角,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
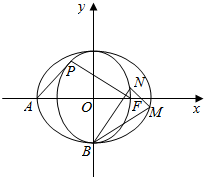 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 0 | 1 |
| P | 0.5 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
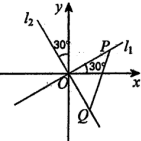 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com