
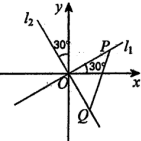
 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.分析 (Ⅰ)通过将点P、Q分别代入l1、l2,利用已知条件计算即可;
(Ⅱ)当直线l垂直于x轴时,易得S△AOB=$\frac{3}{2}$,不符合题意;当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),k≠0,并与椭圆方程联立,利用韦达定理、点到直线的距离计算即可.
解答 解:(Ⅰ)根据题意可得:l1:y=$\frac{\sqrt{3}}{3}$x,l2:y=-$\sqrt{3}$x,
∵点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,
∴y1=$\frac{\sqrt{3}}{3}$x1,y2=-$\sqrt{3}$x2,
又由已知得:l1⊥l2,且|PQ|=2,
∴$({{x}_{1}}^{2}+{{y}_{1}}^{2})$+$({{x}_{2}}^{2}+{{y}_{2}}^{2})$=4,化简得:$\frac{{{x}_{1}}^{2}}{3}$+${{x}_{2}}^{2}$=1,
由x=$\frac{2\sqrt{3}}{3}$x1 ,y=$\sqrt{3}$x2,可得${x}_{1}=\frac{\sqrt{3}}{2}x$,${x}_{2}=\frac{\sqrt{3}}{3}y$,
∴动点M(x,y)的轨迹C的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)当直线l垂直于x轴时,得A(-1,$\frac{3}{2}$)、B(-1,-$\frac{3}{2}$),
此时S△AOB=$\frac{1}{2}$•|AB|•|OF1|=$\frac{1}{2}$×3×1=$\frac{3}{2}$,不符合题意.
当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),k≠0,
联立$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去y得:(3+4k2)x2+8k2x+4k2-12=0.
显然△>0成立,设A(x1,y1)、B(x2,y2),
则x1+x2=-$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$.
又|AB|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}-{x}_{2})^{2}}$
=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{•x}_{2}}$
=$\sqrt{1+{k}^{2}}$$\sqrt{\frac{64{k}^{4}}{(3+4{k}^{2})^{2}}-\frac{4•(4{k}^{2}-12)}{3+4{k}^{2}}}$,
即|AB|=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$,
又圆O的半径r=$\frac{|k×0-0+k|}{\sqrt{1+{k}^{2}}}$=$\frac{|k|}{\sqrt{1+{k}^{2}}}$,
所以S△AOB=$\frac{1}{2}$•|AB|•r=$\frac{1}{2}$•$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$•$\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{6\sqrt{2}}{7}$.
化简得17k4+k2-18=0,即(k2-1)(17k2+18)=0,
解得${{k}_{1}}^{2}$=1,${{k}_{2}}^{2}$=-$\frac{18}{17}$(舍),∴r=$\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{2}}{2}$,
故圆O的方程为:x2+y2=$\frac{1}{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.
第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com