
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
分析 先根据抛物线方程求出焦点坐标和准线方程,运用抛物线的定义和条件可得△AKF为正三角形,F到l的距离为d=2,结合中位线定理,可得|AK|=4,根据正三角形的面积公式可得到答案.
解答 解:抛物线y2=4x的焦点F(1,0),准线为l:x=-1,
由抛物线的定义可得|AF|=|AK|,
由直角三角形的斜边上的中线等于斜边的一半,可得|FK|=|AF|,
即有△AKF为正三角形,
由F到l的距离为d=2,
则|AK|=4,
△AKF的面积是$\frac{\sqrt{3}}{4}$×16=4$\sqrt{3}$.
故选:C.
点评 本题主要考查抛物线的基本性质和直线和抛物线的综合问题.直线和圆锥曲线的综合题是高考的热点要重视.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
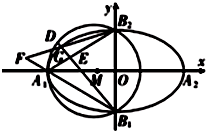 如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).
如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
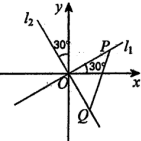 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
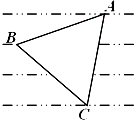 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com