
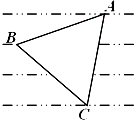
 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米. 分析 由三角函数的定义和已知题意结合图象可得$\frac{3}{sinα}=\frac{9}{cos(30°-α)}$,结合sin2α+cos2α=1可解得sinα的值,进而可得等边△ABC的边长AB=$\frac{3}{sinα}$,代值计算可得.
解答 解:如图所示,在RT△ABD中$\frac{BD}{AB}$=sinα,∴AB=$\frac{BD}{sinα}$=$\frac{3}{sinα}$,
同理在RT△ACE中$\frac{AE}{AC}$=cos∠CAE=cos[90°-(α+60°-)]=cos(30°-α),
∴AC=$\frac{AE}{cos(30°-α)}$=$\frac{9}{cos(30°-α)}$,
∴$\frac{3}{sinα}=\frac{9}{cos(30°-α)}$,即cos(30°-α)=3sinα,
∴$\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα=3sinα,∴$\frac{\sqrt{3}}{2}$cosα=$\frac{5}{2}$sinα,
结合sin2α+cos2α=1可解得sinα=$\frac{\sqrt{21}}{14}$,
∴等边△ABC的边长AB=$\frac{3}{sinα}$=2$\sqrt{21}$
故答案为:2$\sqrt{21}$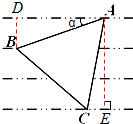
$2\sqrt{21}$
点评 本题考查三角形中的几何运算,涉及三角函数的定义和和差角的三角函数,属中档题.


科目:高中数学 来源: 题型:解答题
 第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.
第一象限内点P在x轴、y轴上的投影分别是A和B,若矩形APBO的周长为定值2m,试证明:过P垂直于AB的直线PC恒过定点,并求出顶点坐标.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一隧道截面由一个长方形和抛物线构成现欲在随道抛物线拱顶上安装交通信息采集装置若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成现欲在随道抛物线拱顶上安装交通信息采集装置若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )| A. | 2$\sqrt{2}$m | B. | 2$\sqrt{3}$m | C. | 4 m | D. | 6 m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com