
 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.分析 (Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,证明BD∥平面EFB1D1,推出MC1∥NP,然后证明PC1∥MN,得到PC1∥平面EFB1D1,利用平面与平面平行的判定定理证明平面EFB1D1∥平面BDC1.
(Ⅱ)连接A1P,说明四边形A1C1CP为平行四边形,证明A1C⊥PC1,推出BD⊥平面A1C1CA,得到BD⊥A1C,然后证明A1C⊥平面BDC1.
解答 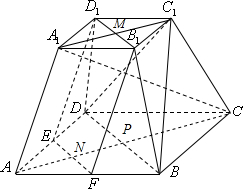 证明:(Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
证明:(Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
由题意,BD∥B1D1,
因为BD?平面EFB1D1,B1D1?平面EFB1D1,所以BD∥平面EFB1D1…(3分)又因为A1B1=a,AB=2a,所以MC1=$\frac{1}{2}$A1C1=$\frac{\sqrt{2}}{2}$a,
又因为E、F分别是AD、AB的中点,所以NP=$\frac{1}{4}$AC=$\frac{\sqrt{2}}{2}$a,
所以MC1=NP,
又因为AC∥A1C1,所以MC1∥NP,
所以四边形MC1PN为平行四边形,
所以PC1∥MN;
因为PC1?平面EFB1D1,MN?平面EFB1D1,所以PC1∥平面EFB1D1,
因为PC1∩BD=P,所以平面EFB1D1∥平面BDC1…(6分)
(Ⅱ)连接A1P,因为A1C1∥PC,A1C1=PC=$\sqrt{2}$a,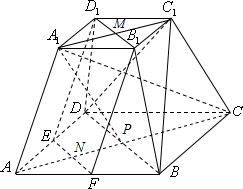
所以四边形A1C1CP为平行四边形,
因为CC1=AA1=PC=$\sqrt{2}$a,所以四边形A1C1CP为菱形,
所以A1C⊥PC1…(9分)
因为MP⊥平面ABCD,MP?平面A1C1CA,
所以平面A1C1CA⊥平面ABCD;
因为BD⊥AC,所以BD⊥平面A1C1CA,
因为A1C?平面A1C1CA,所以BD⊥A1C,
因为PC1∩BD=P,所以A1C⊥平面BDC1.…(12分)
点评 本题考查平面与平面平行的判定定理的应用,直线与平面垂直的判定定理的应用,考查空间想象能力以及逻辑推理能力,


科目:高中数学 来源: 题型:填空题
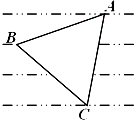 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的是一多面体的三视图(尺寸如图所示,单位:cm),则它的表面积是( )
如图所示的是一多面体的三视图(尺寸如图所示,单位:cm),则它的表面积是( )| A. | (6+3$\sqrt{3}$)cm2 | B. | (12+3$\sqrt{3}$)cm2 | C. | 15cm2 | D. | 9cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com