
分析 (1)设直线AB的方程为x+a=my(m=$\frac{1}{k}$),代入椭圆方程,运用中点坐标公式可得P的坐标,再由两直线垂直的条件,可得m,进而得到k的值;
(2)求出△ABC的面积,化简整理,再令f(m)=m+$\frac{{a}^{2}}{m}$,求出导数,判断单调性,即可得到最大值,注意讨论a的范围.
解答 解:(1)设直线AB的方程为x+a=my(m=$\frac{1}{k}$),
代入椭圆方程得(m2+a2)y2-2may=0
将a=2代入得(m2+4)y2-4my=0,
则AB的中点坐标为P(-$\frac{8}{{m}^{2}+4}$,$\frac{2m}{{m}^{2}+4}$),
B($\frac{2{m}^{2}-8}{{m}^{2}+4}$,$\frac{4m}{{m}^{2}+4}$),C(-$\frac{2{m}^{2}-8}{{m}^{2}+4}$,-$\frac{4m}{{m}^{2}+4}$),
则$\frac{\frac{2m}{{m}^{2}+4}+\frac{4m}{{m}^{2}+4}}{\frac{-8}{{m}^{2}+4}+\frac{2{m}^{2}-8}{{m}^{2}+4}}$=-$\frac{1}{k}$=-m,解得m=$\sqrt{5}$,
所以存在k=$\frac{\sqrt{5}}{5}$,使得|AC|=|BC|;
(2)由(1)得B($\frac{a{m}^{2}-{a}^{3}}{{a}^{2}+{m}^{2}}$,$\frac{2am}{{a}^{2}+{m}^{2}}$),C(-$\frac{a{m}^{2}-{a}^{3}}{{a}^{2}+{m}^{2}}$,-$\frac{2am}{{a}^{2}+{m}^{2}}$),
△ABC的面积S=$\frac{1}{2}$a•$\frac{4am}{{a}^{2}+{m}^{2}}$=$\frac{2{a}^{2}}{m+\frac{{a}^{2}}{m}}$,
令f(m)=m+$\frac{{a}^{2}}{m}$,f′(m)=1-$\frac{{a}^{2}}{{m}^{2}}$=$\frac{{m}^{2}-{a}^{2}}{{m}^{2}}$(1≤m≤2)
当a≥2时,f′(m)≤0,f(m)=m+$\frac{{a}^{2}}{m}$,在[1,2]上单调递减,
所以当m=2时,△ABC的面积的最大值为$\frac{4{a}^{2}}{4+{a}^{2}}$,
当1<a<2时,f(m)=m+$\frac{{a}^{2}}{m}$在[1,a]上单调递减,在[a,2]上单调递增,
所以当m=a时,△ABC的面积的最大值为a.
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的运用,联立直线方程,运用中点坐标公式,以及直线垂直的条件,同时考查三角形的面积的最值,注意运用函数的导数判断单调性,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
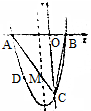
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2 | B. | n2+n | C. | 2n-1 | D. | 2n+1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
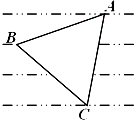 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
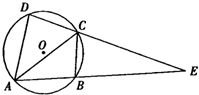 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com