
分析 (1)设T(x,y),由直线的斜率公式,化简整理讨论即可得到曲线方程;
(2)由于0<λ<1,曲线C是焦点在x轴上的椭圆,求得焦点和a-c为最小值,解得λ,进而得到椭圆方程,
(ⅰ)当m=0时,由x=1代入椭圆方程,即可得到P的坐标;(ⅱ)设M(x1,y1),N(x2,y2),联立$\frac{x^2}{4}+\frac{y^2}{3}=1$及x=my+1,运用韦达定理和恒成立思想,即可得到定直线x=4.
解答 解:(1)设T(x,y),则$\frac{y}{x+2}•\frac{y}{x-2}=-λ$,
化简得$\frac{x^2}{4}+\frac{y^2}{4λ}=1(x≠±2)$,又A,B的坐标(-2,0),(2,0)也符合上式,
故曲线C:$\frac{x^2}{4}+\frac{y^2}{4λ}=1(λ>0,λ≠1)$;
当0<λ<1时,曲线C是焦点在x轴上的椭圆,焦点为$(-2\sqrt{1-λ},0),(2\sqrt{1-λ},0)$,
当λ>1时,曲线C是焦点在y轴上的椭圆,焦点为$(0,-2\sqrt{λ-1}),(0,2\sqrt{λ-1})$;
(2)由于0<λ<1,曲线C是焦点在x轴上的椭圆,其焦点为$(-2\sqrt{1-λ},0),(2\sqrt{1-λ},0)$,
椭圆的长轴端点到同侧焦点的距离,是椭圆上的点到焦点的最小距离,
故$2-2\sqrt{1-λ}=1$,∴$λ=\frac{3}{4}$,曲线C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(ⅰ)联立$x=1,\frac{x^2}{4}+\frac{y^2}{3}=1$解得$M(1,\frac{3}{2}),N(1,-\frac{3}{2})$或$N(1,\frac{3}{2}),M(1,-\frac{3}{2})$,
当$M(1,\frac{3}{2}),N(1,-\frac{3}{2})$时,$AM:y=\frac{1}{2}(x+2),BN:y=\frac{3}{2}(x-2)$,解得P(4,3),
当$N(1,\frac{3}{2}),M(1,-\frac{3}{2})$时,由对称性知,P(4,-3),
所以点P坐标为(4,3)或(4,-3);
(ⅱ)以下证明当m变化时,点P总在直线x=4上.
设M(x1,y1),N(x2,y2),联立$\frac{x^2}{4}+\frac{y^2}{3}=1$及x=my+1,
消去x得:(3m2+4)y2+6my-9=0,${y_1}+{y_2}=-\frac{6m}{{3{m^2}+4}},{y_1}{y_2}=-\frac{9}{{3{m^2}+4}}$,
直线$AM:y=\frac{y_1}{{{x_1}+2}}(x+2),BN:y=\frac{y_2}{{{x_2}-2}}(x-2)$,
消去y得$x=\frac{{2{y_1}({x_2}-2)+2{y_2}({x_1}+2)}}{{{y_2}({x_1}+2)-{y_1}({x_2}-2)}}=\frac{{4m{y_1}{y_2}-2{y_1}+6{y_2}}}{{{y_1}+3{y_2}}}$,
以下只需证明$\frac{{4m{y_1}{y_2}-2{y_1}+6{y_2}}}{{{y_1}+3{y_2}}}=4?4m{y_1}{y_2}-6({y_1}+{y_2})=0$(※) 对于m∈R恒成立.
而$4m{y_1}{y_2}-6({y_1}+{y_2})=4m•(-\frac{9}{{3{m^2}+4}})-6•(-\frac{6m}{{3{m^2}+4}})=\frac{{-36{m^2}+36{m^2}}}{{3{m^2}+4}}=0$
所以(※)式恒成立,即点P横坐标总是4,点P总在直线x=4上,
故存在直线l':x=4,使P总在直线l'上.
点评 本题考查曲线方程的求法,主要考查椭圆的性质和方程的运用.联立直线方程运用韦达定理以及恒成立思想的运用,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 0 | 1 |
| P | 0.5 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
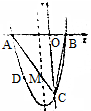
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
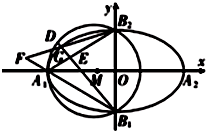 如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).
如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
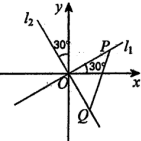 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com