
分析 依题意,可得$\frac{{({a}_{n}-2)}^{2}}{2}$=2-an+1≥0,进一步分析可得an<2,再对$\frac{{({a}_{n}-2)}^{2}}{2}$=2-an+1两边取对数,利用等比数列的通项公式与对数的运算性质即可求得答案.
解答 解:因为an+1=$\frac{1}{2}{a}_{n}$(4-an)=-$\frac{({a}_{n}-2)^{2}}{2}$+2,
所以$\frac{{({a}_{n}-2)}^{2}}{2}$=2-an+1≥0,即an+1≤2,
若an+1=2,即$\frac{1}{2}{a}_{n}$(4-an)=2,故an=2,这与a1=$\frac{3}{2}$矛盾,
所以,an+1<2,即an<2,
所以对$\frac{{({a}_{n}-2)}^{2}}{2}$=2-an+1两边取对数,得lg(2-an+1)=2lg(2-an)-lg2,
变形得:lg(2-an+1)-lg2=2[lg(2-an)-lg2],
∴lg(2-an)-lg2=2n-1•(-2lg2)=-2n•lg2=lg${2}^{-{2}^{n}}$,
解得:an=2-${2}^{1-{2}^{n}}$.
故答案为:an=2-${2}^{1-{2}^{n}}$.
点评 本题考查数列递推关系式的应用,分析得到an<2,且对$\frac{{({a}_{n}-2)}^{2}}{2}$=2-an+1两边取对数是关键,也是难点,考查等价转化思想与推理运算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}$(1-4-n) | B. | $\frac{32}{3}$(1-2-n) | C. | 16(1-4-n) | D. | 16(1-2-n) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
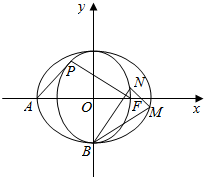 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
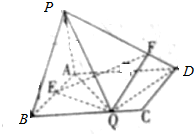 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
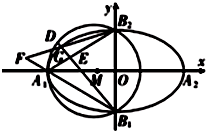 如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).
如图,已知A1,A2,B1,B2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点,△A1B1B2的外接圆为圆M,椭圆C过点(-1,$\frac{\sqrt{6}}{3}$),($\frac{3}{2}$,$\frac{1}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com