
【题目】如图所示,四棱锥P﹣ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
(I)求证:平面PDE⊥平面PAC;
(Ⅱ)求直线PC与平面PDE所成的角的正弦值.
【答案】解:(I)以点C为坐标原点,以直线CD,CB,CP分别为x,y,z轴建立空间直角坐标系C﹣xyz,
则C(0,0,0),A(2,1,0),B(0,3,0),P(0,0,2),D(2,0,0),E(1,2,0).
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴DE⊥CA,DE⊥CP,
又CP∩CA=C,AC平面PAC,CP平面PAC,
∴DE⊥平面PAC,∵DE平面PDE,
∴平面PDE⊥平面PAC.
(Ⅱ) ![]() ,
,
设 ![]() 是平面PDE的一个法向量,则
是平面PDE的一个法向量,则 ![]() ,
,
∴ ![]() ,
,
令x=2,则y=1,z=2,即 ![]() ,
,
∴ ![]() =4,|
=4,| ![]() |=3,|
|=3,| ![]() |=2,
|=2,
∴cos< ![]() >=
>= 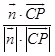 =
= ![]() .
.
∴直线PC与平面PDE所成的角的正弦值为 ![]() .
.
【解析】(I)点C为坐标原点建立空间直角坐标系,求出向量 ![]() ,
, ![]() ,
, ![]() 的坐标,根据数量积得出DE⊥AC,DE⊥CP,故而DE⊥平面PAC,于是平面PDE⊥平面PAC;(II)求出平面PDE的法向量
的坐标,根据数量积得出DE⊥AC,DE⊥CP,故而DE⊥平面PAC,于是平面PDE⊥平面PAC;(II)求出平面PDE的法向量 ![]() ,计算
,计算 ![]() 与
与 ![]() 的夹角,则直线PC与平面PDE所成的角的正弦值等于|cos<
的夹角,则直线PC与平面PDE所成的角的正弦值等于|cos< ![]() >|.
>|.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是 . (填序号)
①MB∥平面A1DE;
②|BM|是定值;
③A1C⊥DE.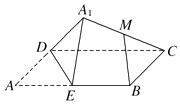
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:存在定点![]() ,使得函数
,使得函数![]() 图象上任意一点
图象上任意一点![]() 关于
关于![]() 点对称的点
点对称的点![]() 也在函数
也在函数![]() 的图象上,并求出点
的图象上,并求出点![]() 的坐标;
的坐标;
(2)定义![]() ,其中
,其中![]() 且
且![]() ,求
,求![]() ;
;
(3)对于(2)中的![]() ,求证:对于任意
,求证:对于任意![]() 都有
都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x﹣1),g(x)=loga(3﹣x)(a>0且a≠1)
(1)求函数h(x)=f(x)﹣g(x)的定义域;
(2)利用对数函数的单调性,讨论不等式f(x)≥g(x)中x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为 ![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com