练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．（x-2）（x+1）5的展开式中，x3的系数是-10（用数字填写答案）

    分析 求出（x+1）5展开式的含x2与x3项的系数，再计算（x-2）（x+1）5展开式中x3的系数．

    解答 解：（x+1）5展开式的通项公式为Tr+1=C5r•x5-r，
    令5-r=2，解得r=3，
    所以T4=C53•x2=10x2；
    令5-r=3，解得r=2，
    所以T3=C52•x3=10x3；
    所以（x-2）（x+1）5展开式中x3的系数为
    10×1+10×（-2）=-10．
    故答案为：-10．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=x2sin$\frac{πx}{2}$，数列{an}中，an=f（n）-f（n+1）（n∈N*），则数列{an}的前100项之和S100=-10200．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

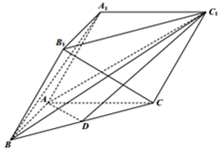    12．如图，在三棱柱ABC-A1B1C1中，D为BC的中点，∠BAC=90°，∠A1AC=60°，AB=AC=AA1=2．
    （Ⅰ）求证：A1B∥平面ADC1；
    （Ⅱ）当BC1=4时，求直线B1C与平面ADC1所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．一组数据的平均数是4.8，方差是3.6，若将这组数据中的每一个数据都加上60，得到一组新数据，则所得新数据的平均数和方差分别是（　　）
    A．55.2，3.6B．55.2，56.4C．64.8，63.6D．64.8，3.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知函数f（x）=ex+a•e-x+2（a∈R，e为自然对数的底数），若y=f（x）与y=f（f（x））的值域相同，则a的取值范围是（　　）
    A．a＜0B．a≤-1C．0＜a≤4D．a＜0或0＜a≤4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．数列{an}满足a2=2，an+2+（-1）n+1an=1+（-1）n（n∈N*），S n为数列{an}前n项和，S100=（　　）
    A．5100B．2550C．2500D．2450

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在一次爱心捐款活动中，小李为了了解捐款数额是否和居民自身的经济收入有关，随机调查了某地区的100个捐款居民每月平均的经济收入．在捐款超过100元的居民中，每月平均的经济收入没有达到2000元的有60个，达到2000元的有20个；在捐款不超过100元的居民中，每月平均的经济收入没有达到2000元的有10个．
    （Ⅰ）在下图表格空白处填写正确数字，并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关？
    （Ⅱ）将上述调查所得到的频率视为概率．现在从该地区大量居民中，采用随机抽样方法每次抽取1个居民，共抽取3次，记被抽取的3个居民中经济收入达到2000元的人数为X，求P（X=2）和期望EX的值．
    每月平均经济收入达到2000元每月平均经济收入没有达到2000元合计
    捐款超过
    100元
    捐款不超
    过100元
    合计
    参
    考
    数
    据    		 当x2≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联；
     当x2＞2.706时，有90%的把握判定变量A，B有关联；
     当x2＞3.841时，有95%的把握判定变量A，B有关联；
     当x2＞6.635时，有99%的把握判定变量A，B有关联．
    附：X2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．偶函数f（x）是定义域为R上的可导函数，当x≥0时，都有f'（x）＜2x成立，则不等式f（x-1）+2x＞f（x）+1的解集是（　　）
    A．$\left\{{\left.x\right|x＜\frac{1}{2}}\right\}$B．$\left\{{\left.x\right|x＞\frac{1}{2}}\right\}$C．{x|x≠$\frac{1}{2}$}D．实数集R

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知数列{an}满足a1=1，an+1=$\left\{\begin{array}{l}{{a}_{n}+1，{a}_{n}＜3}\\{\frac{{a}_{n}}{3}，{a}_{n}≥3}\end{array}\right.$，则数列{an}的前12项和S12=24．

    查看答案和解析>>

    同步练习册答案