
| A. | 5100 | B. | 2550 | C. | 2500 | D. | 2450 |
分析 数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),n=2k(k∈N*)时,a2k+2-a2k=2,因此数列{a2k}为等差数列,首项为2,公差为2.n=2k-1(k∈N*)时,a2k+1+a2k-1=0.通过分组求和,利用等差数列的求和公式即可得出.
解答 解:数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),
n=2k(k∈N*)时,a2k+2-a2k=2,因此数列{a2k}为等差数列,首项为2,公差为2.
n=2k-1(k∈N*)时,a2k+1+a2k-1=0.
∴S100=(a1+a3+…+a97+a99)+(a2+a4+…+a100)
=0+2×50+$\frac{50×49}{2}×2$=2550.
故选:B.
点评 本题考查了等差数列的通项公式与求和公式、数列递推关系、分类讨论方法、分组求和,考查了推理能力与计算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
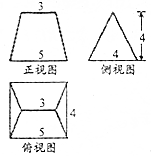
| A. | $\frac{113}{3}$ | B. | 35 | C. | $\frac{104}{3}$ | D. | $\frac{107}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 504 | B. | 1008 | C. | 1009 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
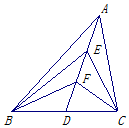 如图,在△ABC中,D为BC的中点,E,F为AD上的两个三等分点.若$\overrightarrow{BE}•\overrightarrow{CE}=\frac{7}{8}$,$BC=\frac{{\sqrt{26}}}{2}$,则$\overrightarrow{BF}•\overrightarrow{CF}$=-$\frac{17}{8}$.
如图,在△ABC中,D为BC的中点,E,F为AD上的两个三等分点.若$\overrightarrow{BE}•\overrightarrow{CE}=\frac{7}{8}$,$BC=\frac{{\sqrt{26}}}{2}$,则$\overrightarrow{BF}•\overrightarrow{CF}$=-$\frac{17}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 6 | C. | 8 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com