
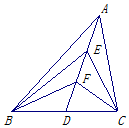
 如图,在△ABC中,D为BC的中点,E,F为AD上的两个三等分点.若$\overrightarrow{BE}•\overrightarrow{CE}=\frac{7}{8}$,$BC=\frac{{\sqrt{26}}}{2}$,则$\overrightarrow{BF}•\overrightarrow{CF}$=-$\frac{17}{8}$.
如图,在△ABC中,D为BC的中点,E,F为AD上的两个三等分点.若$\overrightarrow{BE}•\overrightarrow{CE}=\frac{7}{8}$,$BC=\frac{{\sqrt{26}}}{2}$,则$\overrightarrow{BF}•\overrightarrow{CF}$=-$\frac{17}{8}$. 分析 根据向量的加减的几何意义和向量的数量积即可求出.
解答 解:D为BC的中点,E,F为AD上的两个三等分点,
∴$\overrightarrow{BE}$=$\overrightarrow{BD}$+$\overrightarrow{DE}$,$\overrightarrow{CE}$=-$\overrightarrow{BD}$+$\overrightarrow{DE}$,
∴$\overrightarrow{BE}$•$\overrightarrow{CE}$=${\overrightarrow{DE}}^{2}$-${\overrightarrow{BD}}^{2}$=$\frac{7}{8}$,
∴$\overrightarrow{DE}$2=$\frac{7}{8}$+$\frac{13}{4}$=$\frac{33}{8}$,
∵$\overrightarrow{BF}$=$\overrightarrow{BD}$+$\overrightarrow{DF}$=$\overrightarrow{BD}$+$\frac{1}{2}$$\overrightarrow{DE}$,$\overrightarrow{CF}$=-$\overrightarrow{BD}$+$\frac{1}{2}$$\overrightarrow{DE}$,
∴$\overrightarrow{BF}$•$\overrightarrow{CF}$=$\frac{1}{4}$${\overrightarrow{DE}}^{2}$-${\overrightarrow{BD}}^{2}$=$\frac{1}{4}$×$\frac{33}{8}$-$\frac{13}{4}$=-$\frac{17}{8}$,
故答案为:-$\frac{17}{8}$.
点评 本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 55.2,3.6 | B. | 55.2,56.4 | C. | 64.8,63.6 | D. | 64.8,3.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5100 | B. | 2550 | C. | 2500 | D. | 2450 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每月平均经济收入达到2000元 | 每月平均经济收入没有达到2000元 | 合计 | |
| 捐款超过 100元 | |||
| 捐款不超 过100元 | |||
| 合计 |
| 参 考 数 据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\left.x\right|x<\frac{1}{2}}\right\}$ | B. | $\left\{{\left.x\right|x>\frac{1}{2}}\right\}$ | C. | {x|x≠$\frac{1}{2}$} | D. | 实数集R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
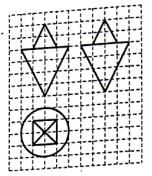
| A. | $\frac{16}{3}(π+1)$ | B. | $\frac{8}{3}(2π+1)$ | C. | 8(2π+1) | D. | 16(π+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com