Question

【题目】已知圆C：，直线：．

（1）若直线被圆C截得的弦长为 ，求实数的值；

（2）当t =1时，由直线上的动点P引圆C的两条切线，若切点分别为A，B，则直线AB是否恒过一个定点？若存在，求出该定点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）t =11；（2）

【解析】

（1）根据垂径定理列式求实数的值；（2）先根据切点A，B在以CP为直径的圆，再根据两圆方程得切点弦方程，最后根据动点P在直线上，确定切点弦过定点.

(1)圆C的方程可化为 ,

则圆心C到直线的距离为

又弦长为 ，则

即 ，解得t =11.

（2）当t =1时，圆C的方程为①

则圆心为C（3，5），半径 ，圆C与直线相离

假设在直线AB上存在一个定点满足条件，设动点P（m，n），由已知得PA⊥AC，PB⊥BC

则A，B在以CP为直径的圆（x﹣3）（x﹣m）+（y﹣5）（y﹣n）=0

即②

①﹣②得，直线AB的方程为（m﹣3）x+（n﹣5）y﹣3m﹣5n﹣6=0③

又点P（m，n）在直线上，则m+3n+12=0，即m=﹣3n﹣12，代入③式

得（﹣3n﹣15）x+（n﹣5）y+4n+30=0

即直线AB的方程为15x+5y﹣30+n（3x﹣y﹣4）=0

因为上式对任意n都成立，故 ，得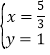

故直线AB恒过一个定点，定点坐标为