练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，已知A=，．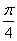

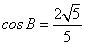      (I)求cosC的值；

      (Ⅱ)若BC=2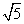，D为AB的中点，求CD的长．


    （Ⅰ）且，∴    …………2分

              ……………………………………………4分

           …………………………6分

        （Ⅱ）由（Ⅰ）可得     ……………………8分

    由正弦定理得，即，解得．  ………………………………10分

        在中，，所以


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设定义在上的函数满足，若，则

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知表示不超过实数的最大整数，如：．定义，求（　　）

    A. 1006            B.1007          C. 1008          D.2014

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn为等差数列{an}的前n项和，若a1=1，a3=5，Sk+2﹣Sk=36，则k的值为（　　）

    　

    A．

    8

    B．

    7

    C．

    6

    D．

    5

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    （3x+）6的展开式中常数项为　　（用数字作答）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f（x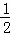）=ax2﹣（2a+1）x+2lnx（a＞0）．

    （Ⅰ） 若a≠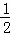，求函数f（x）的单调区间；

    （Ⅱ）当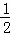＜a＜1时，判断函数f（x）在区间[1，2]上有无零点？写出推理过程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二项式的展开式的各项系数的和为，所有二项式系数的和为，则的值为          ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设全集U=R，A=，B={ x∈R︱x 2+ x－6=0}，则下图中阴影表示的集合为          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


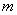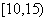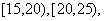
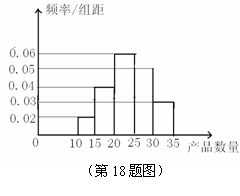
    为了调查某厂数万名工人独立生产某种产品的能力，随机抽查了位工人某天独立生产该产品的数量，产品数量的分组区间为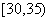，，频率分布直方图如图所示，已知独立生产的产品数量在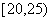之间的工人有6位．

    （Ⅰ）求；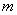

    （Ⅱ）工厂规定：若独立生产能力当日不小于25，则该工人当选今日“生产之星”．

     若将这天独立生产该产品数量的频率视为概率，随机从全厂工人中抽取3人，

    这3人中当日“生产之星”人数为X，求X的分布列及数学期望．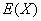

    查看答案和解析>>

    同步练习册答案