
已知函数f(x)=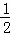 ax2﹣(2a+1)x+2lnx(a>0).
ax2﹣(2a+1)x+2lnx(a>0).
(Ⅰ) 若a≠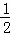 ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(Ⅱ)当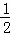 <a<1时,判断函数f(x)在区间[1,2]上有无零点?写出推理过程.
<a<1时,判断函数f(x)在区间[1,2]上有无零点?写出推理过程.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
某品牌汽车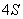 店对最近
店对最近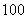 位采用分期付款的购车者进行统计,统计结果如下表示所示:
位采用分期付款的购车者进行统计,统计结果如下表示所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 |
| 10 |
|
已知分3期付款的频率为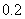 ,
,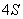 店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为
店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为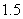 万元;分4期或5期付款,其利润为
万元;分4期或5期付款,其利润为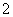 万元,用
万元,用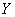 表示经销一辆汽车的利润。
表示经销一辆汽车的利润。
(1)求上表中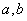 的值;
的值;
(2)若以频率作为概率,求事件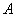 :“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率
:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率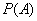 ;
;
(3)求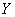 的分布列及数学期望
的分布列及数学期望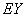 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为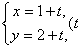 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点
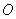 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,圆
轴的正半轴为极轴的极坐标系下,圆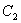 的方程为
的方程为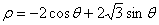 .
.
(Ⅰ)求直线 的普通方程和圆
的普通方程和圆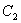 的圆心的极坐标;
的圆心的极坐标;
(Ⅱ)设直线 和圆
和圆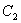 的交点为
的交点为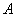 、
、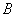 ,求弦
,求弦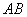 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com