
分析 (1)利用二倍角公式及变形,两角和的正弦公式化简解析式,由三角函数的周期公式求出f(x)的最小正周期;
(2)由x∈[0,π]求出x+$\frac{π}{4}$的范围,由正弦函数的单调性求出函数f(x)在区间[0,π]上的单调减区间.
解答 解:(1)由题意得,f(x)=$\sqrt{2}$sin$\frac{x}{2}$cos$\frac{x}{2}$-$\sqrt{2}$sin2$\frac{x}{2}$
=$\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$(1-cosx)=$sin(x+\frac{π}{4})-\frac{\sqrt{2}}{2}$,
∴f(x)的最小正周期T=$\frac{2π}{1}=2π$;
(2)由x∈[0,π]得,x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],
由$\frac{π}{2}≤x+\frac{π}{4}≤\frac{5π}{4}$得,$\frac{π}{4}≤x≤π$,
∴f(x)在区间[0,π]上的单调减区间是$[\frac{π}{4},π]$.
点评 本题考查了二倍角公式及变形,两角和的正弦公式,以及正弦函数的图象与性质,考查整体思想,化简、变形能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
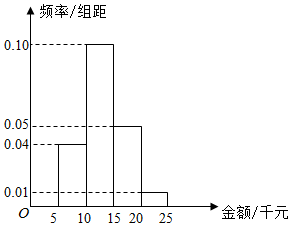 某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图.
某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
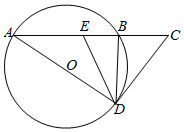 如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.
如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com