Question

11．如图，O是以AB为直径的圆，且AB=4，点P，Q在圆O上（与A，B不重合）
（1）若PB=2，求$\overrightarrow{PA}$•$\overrightarrow{AB}$；
（2）若∠PAB=30．且点Q与P关于直线AB对称，$\overrightarrow{OA}$=a，$\overrightarrow{OP}$=b，求$\overrightarrow{OQ}$．

Answer 1

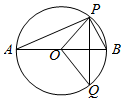
分析 （1）根据题意，利用平面向量的线性运算与勾股定理，即可求出$\overrightarrow{PA}$•$\overrightarrow{AB}$的值；
（2）建立适当的平面直角坐标系，利用平面向量的坐标表示，即可求出$\overrightarrow{OQ}$的坐标表示．

解答 解：（1）根据题意，AB为圆O的直径，∴PA⊥PB，
∴$\overrightarrow{PA}$•$\overrightarrow{AB}$=$\overrightarrow{PA}$•（$\overrightarrow{PB}$-$\overrightarrow{PA}$）
=$\overrightarrow{PA}$•$\overrightarrow{PB}$-${\overrightarrow{PA}}^{2}$
=0-${\overrightarrow{PA}}^{2}$
=-（${\overrightarrow{AB}}^{2}$-${\overrightarrow{PB}}^{2}$）
=-（4²-2²）
=-12；
（2）建立平面直角坐标系，如图所示
∠PAB=30°，且点Q与P关于直线AB对称，
∴$\overrightarrow{OA}$=$\overrightarrow{a}$=（-2，0），
$\overrightarrow{OP}$=$\overrightarrow{b}$=（2cos60°，2sin60°）=（1，$\sqrt{3}$）；
又$\overrightarrow{OQ}$=（1，-$\sqrt{3}$），
∴$\overrightarrow{OQ}$=x$\overrightarrow{OA}$+y$\overrightarrow{OP}$，x、y∈R；
∴（1-$\sqrt{3}$）=（-2x+y，$\sqrt{3}$y），
即$\left\{\begin{array}{l}{-2x+y=1}\\{\sqrt{3}y=-\sqrt{3}}\end{array}\right.$，
解得x=-1，y=-1；
∴$\overrightarrow{OQ}$=-$\overrightarrow{OA}$-$\overrightarrow{OP}$=-$\overrightarrow{a}$-$\overrightarrow{b}$．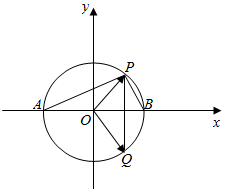

点评 本题考查了平面向量的坐标表示与平面向量的数量积的应用问题，是综合性题目．