
 在长方体ABCD-A1B1C1D1中,B1D与平面A1BC1交于H点,E是DD1的中点,$\overrightarrow{BF}=3\overrightarrow{FD}$.
在长方体ABCD-A1B1C1D1中,B1D与平面A1BC1交于H点,E是DD1的中点,$\overrightarrow{BF}=3\overrightarrow{FD}$.分析 (1)连接B1D1交A1C1于O,O为A1C1的中点,连接AC交BD于O1,O1是BD的中点,连接D1O1,证明OB∥D1O1,证明EF∥OB,即可证明以EF∥平面A1BC1
(2)证明BH=2HO,又BO为三角形A1BC1的中线,推出H为三角形A1BC1的重心.
解答 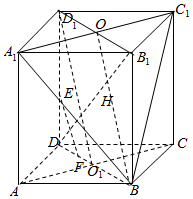 证明:(1)连接B1D1交A1C1于O,O为A1C1的中点,
证明:(1)连接B1D1交A1C1于O,O为A1C1的中点,
连接AC交BD于O1,O1是BD的中点,连接D1O1,
在长方体中,OD1∥BO1且OD1=BO1,所以BOD1O1为平行四边形,所以OB∥D1O1,
又$\overrightarrow{BF}=3\overrightarrow{FD}$,所以F为DO1的中点,E为DD1的中点,所以EF∥D1O1
EF∥OB,OB?平面A1BC1,EF?平面A1BC1,
所以EF∥平面A1BC1
(2)在矩形BB1D1D中,B1D∩B1D=M,M∈B1D且M∈BO?平面A1BC1,
所以M为直线B1D与平面A1BC1的公共点,所以M点就是H点.
又在矩形BB1D1D中,三角形B1OH相似于三角形BDH,
又${B_1}O=\frac{1}{2}BD$,所以BH=2HO,又BO为三角形A1BC1的中线,
所以H为三角形A1BC1的重心.
点评 本题考查直线与平面平行的判定定理的应用,空间点的位置关系,考查空间想象能力以及计算能力.是课本题改编(课本79页题改编).


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | $\sqrt{41}$ | C. | 6 | D. | $\sqrt{61}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{5}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{13}$ | B. | 13 | C. | $\sqrt{13}$ | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| T(分钟) | 25 | 30 | 35 | 40 |
| 频数(次) | 20 | 30 | 40 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com