
| T(分钟) | 25 | 30 | 35 | 40 |
| 频数(次) | 20 | 30 | 40 | 10 |
分析 (Ⅰ)由统计结果可得T的频率分布,从而得到以频率估计概率得T的分布列,由此能求出随机变量T的分布列与数学期望ET.
(Ⅱ)设T1,T2分别表示往、返所需时间,T1,T2的取值相互独立,且与T的分布列相同.设事件A表示“刘教授共用时间不超过120分钟”,由于讲座时间为50分钟,所以事件A对应于“刘教授在途中的时间不超过70分钟”.由此能求出刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
解答 解:(Ⅰ)由统计结果可得T的频率分布为
| T(分钟) | 25 | 30 | 35 | 40 |
| 频率 | 0.2 | 0.3 | 0.4 | 0.1 |
| T | 25 | 30 | 35 | 40 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意互斥事件概率加法公式的合理运用.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
 在长方体ABCD-A1B1C1D1中,B1D与平面A1BC1交于H点,E是DD1的中点,$\overrightarrow{BF}=3\overrightarrow{FD}$.
在长方体ABCD-A1B1C1D1中,B1D与平面A1BC1交于H点,E是DD1的中点,$\overrightarrow{BF}=3\overrightarrow{FD}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{6}$ | B. | 向左平移$\frac{π}{6}$ | C. | 向左平移$\frac{π}{3}$ | D. | 向右平移$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 242 | B. | 121 | C. | 244 | D. | 122 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面α内任意直线都与直线a异面 | B. | 平面α内不存在与直线a平行的直线 | ||
| C. | 平面α内的直线都与直线a相交 | D. | 直线a与平面α一定有公共点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
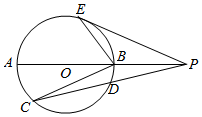 如图,半径为2的⊙O的直径AB的延长线与弦CD的延长线相交与点P,PE为⊙O的切线,E为切点,$\overrightarrow{BE}$=2$\overrightarrow{BD}$,若PB=2,PD=$\frac{5}{2}$,∠PEB=30°.
如图,半径为2的⊙O的直径AB的延长线与弦CD的延长线相交与点P,PE为⊙O的切线,E为切点,$\overrightarrow{BE}$=2$\overrightarrow{BD}$,若PB=2,PD=$\frac{5}{2}$,∠PEB=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com