
分析 (1)假设存在x1,x2∈[-$\frac{3}{2}$,-a],使得f(x1)>g(x2),即有f(x)max>g(x)min,分别求得f(x)、g(x)的导数,判断单调性,可得最值,解不等式可得a的范围,与已知a的范围比较,即可判断存在;
(2)当与直线8x+y+15=0平行的直线与曲线y=g(x)相切时,切点P到直线的距离最小,由导数的几何意义可得P的坐标,由点到直线的距离公式可得所求最小距离.
解答 解:(1)假设存在x1,x2∈[-$\frac{3}{2}$,-a],使得f(x1)>g(x2),
可得f(x)max>g(x)min,
由函数f(x)=$\frac{a{e}^{x+2}}{2+x}$(a≠0)的导数为f′(x)=$\frac{a{e}^{x+2}(x+1)}{(x+2)^{2}}$,
由x∈[-$\frac{3}{2}$,-a],可得x+1∈[-$\frac{1}{2}$,1-a],又1<a<$\frac{3}{2}$,可得1-a<0,
则f′(x)<0,f(x)在[-$\frac{3}{2}$,-a]递减,可得f(x)max=f(-$\frac{3}{2}$);
由g(x)=$\frac{1}{x+2}$+2ln(x+2)的导数为g′(x)=-$\frac{1}{(x+2)^{2}}$+$\frac{2}{x+2}$=$\frac{2x+3}{(x+2)^{2}}$,
由x∈[-$\frac{3}{2}$,-a],可得g′(x)>0,g(x)递增,
可得g(x)min=g(-$\frac{3}{2}$),
由f(x)max>g(x)min,可得$\frac{a{e}^{\frac{1}{2}}}{\frac{1}{2}}$>$\frac{1}{\frac{1}{2}}$+2ln$\frac{1}{2}$,
化简可得a>$\frac{1-ln2}{{e}^{\frac{1}{2}}}$,
由$\frac{1-ln2}{{e}^{\frac{1}{2}}}$∈(0,1),又1<a<$\frac{3}{2}$,
可得在1<a<$\frac{3}{2}$,存在x1,x2∈[-$\frac{3}{2}$,-a],使得f(x1)>g(x2);
(2)设与直线8x+y+15=0平行的切线与曲线y=g(x)相切的切点P(m,n),
可得$\frac{2m+3}{(m+2)^{2}}$=-8,(m>-2)
解得m=-$\frac{7}{4}$(-$\frac{5}{2}$舍去),
即有切点P(-$\frac{7}{4}$,4-4ln2),
可得P到直线8x+y+15=0的距离为d=$\frac{|-14+4-4ln2+15|}{\sqrt{64+1}}$
=$\frac{|5-4ln2|}{\sqrt{65}}$=$\frac{(5-4ln2)\sqrt{65}}{65}$,
则点P到直线8x+y+15=0的最小距离为$\frac{(5-4ln2)\sqrt{65}}{65}$,
此时点P的坐标(-$\frac{7}{4}$,4-4ln2).
点评 本题考查导数的运用:求切线的斜率和单调区间,考查存在性问题的解法,同时考查曲线上点到直线的距离的最值的求法,注意运用直线和曲线相切,运用点到直线的距离公式,属于中档题.


科目:高中数学 来源: 题型:解答题
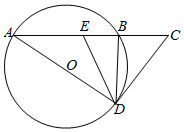 如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.
如图,A,B是圆O上两点,延长AB至点C,满足AB=2BC=2,过C作直线CD与圆O相切于点D,∠ADB的平分线交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{5}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com