Question

5．某一天，一船从南岸出发，向北岸横渡．根据测量，这一天水流速度为3km/h，方向正东，风的方向为北偏西30°，受风力影响，静水中船的漂行速度为3km/h，若要使该船由南向北沿垂直与河岸的方向以2$\sqrt{3}$km/h的速度横渡，求船本身的速度大小及方向．

Answer 1

分析 根据题意建立直角坐标系，设$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{x}$、$\overrightarrow{c}$分别是水速、风影响船速、船速、最后合成之实际船速，画出图形，由题意列出方程求出$\overrightarrow{x}$，由向量的模求出船实际航行的速度，由反三角函数求出方向．

解答 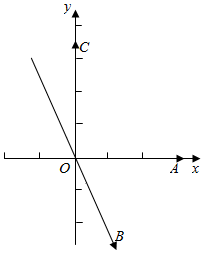解建立如图所示的直角坐标系，
设$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{x}$、$\overrightarrow{c}$分别是水速、风影响船速、船速、最后合成之实际船速，如图$\overrightarrow{OA}=\overrightarrow{a}$，$\overrightarrow{OB}=\overrightarrow{b}$，$\overrightarrow{OC}=\overrightarrow{c}$，
由题意得，$\overrightarrow{a}$=（3，0），$\overrightarrow{b}$=（$\frac{3}{2}$，$-\frac{3\sqrt{3}}{2}$），$\overrightarrow{c}$=（0，$2\sqrt{3}$）
[单位：km/h]，
∵$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{x}$=$\overrightarrow{c}$，∴$\overrightarrow{x}$=$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$=（$-\frac{9}{2}$，$\frac{7\sqrt{3}}{2}$）
∴|$\overrightarrow{x}$|=$\sqrt{（-\frac{9}{2}）^{2}+（{\frac{7\sqrt{3}}{2}）}^{2}}$=$\sqrt{57}$，
由sinα=$\frac{\frac{9}{2}}{\sqrt{57}}$=$\frac{9\sqrt{57}}{114}$得，$\overrightarrow{x}$方向：北偏西arcsin$\frac{9\sqrt{57}}{114}$，
∴船本身的速度大小及方向分别是$\sqrt{57}$、北偏西arcsin$\frac{9\sqrt{57}}{114}$．

点评 本题考查了向量在物理中的应用，向量加减混合运算以及几何意义，解题时注意船在静水中速度，水流速度和船的实际速度三个概念的区分，考查数形结合思想．